Benutzer:Buss-Haskert/Terme 8E: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=== Flächeninhalte mit Termen beschreiben === ===1. Ausmultiplizieren und Ausklammern (• vor der Klammer )=== {{Box|Wiederholung|Skizziere das Rechteck in dein Heft und berechne den Flächeninhalt des gesamten Rechtecks. links|300px Findest du verschiedene Möglichkeiten? Notiere im Heft.|Arbeitsmethode}} Vergleiche deine Ideen mit denen im nachfolgenden Video: {{#ev:youtube|r7uwFsEcxGI}} Wie…“) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 51: | Zeile 51: | ||
{{Box|Übung 1: Verteilungsgesetz: Rechnen mit Rechtecken|Löse zur Übung die nachfolgenden LearningApps.|Üben}} | {{Box|Übung 1: Verteilungsgesetz: Rechnen mit Rechtecken|Löse zur Übung die nachfolgenden LearningApps.|Üben}} | ||
{{LearningApp|app=pv9ujh6r520|width=100%|height=400px}} | {{LearningApp|app=pv9ujh6r520|width=100%|height=400px}} | ||
====1.1 Ausmultiplizieren==== | |||
Durch Ausmultiplizieren wird ein Produkt in eine Summe umgewandelt, die Klammern werden also aufgelöst. | |||
{{Box|Hefteintrag: Ausmultiplizieren|Beim Ausmultiplizieren wird jeder Summand in der Klammer mit dem Faktor vor/nach der Klammer multipliziert. | |||
Tipp: "Jedem die Hand geben" [[Datei:Händedruck grau.png|rahmenlos|50x50px]]|Arbeitsmethode}} | |||
Beispiele: | |||
<div class="grid"> | |||
<div class="width-1-2"> | |||
a) | |||
[[Datei:Rechteck 4.png|rahmenlos|alternativtext=|ohne]] | |||
Produkt Summe | |||
2⋅(x + 5) = 2⋅x + 2⋅5 | |||
= 2x + 10 </div> | |||
<div class="width-1-2"> | |||
b) [[Datei:Rechteck 5.png|rahmenlos|alternativtext=|ohne]] | |||
Produkt Summe | |||
(a + 3b)⋅2c = a⋅2c + 3b⋅2c | |||
= 2ac + 6bc </div> | |||
</div> | |||
{{#ev:youtube|bEeTAotb7hg|800|center}} | |||
{{Box|Übung 5 Überflüssige Malpunkte|Um Produktterme so einfach wie möglich zu schreiben, dürfen überflüssige Malpunkte weggelassen werden. Dies sind Malpunkte zwischen einer Zahl und einer Variablen und zwischen einer Zahl oder Variablen und einer Klammer.Markiere die überflüssigen Malpunkte in den Termen.|Üben}} | |||
{{LearningApp|app=pynxyt0qk20|width=100%|height=300px}} | |||
{{Box|Übung 6 Ausmultiplizieren|Löse die Klammern auf und vereinfache den Term so weit wie möglich.|Üben}} | |||
<div class="grid"> | |||
<div class="width-1-2">{{LearningApp|app=pg8vo75in20|width=100%|height=600px}}</div><div class="width-1-2">{{LearningApp|app=p7nuszkut19|width=100%|height=600px}}</div> | |||
</div> | |||
====1.2 Ausklammern==== | |||
Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt. | |||
Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben. | |||
<br> | |||
{{#ev:youtube|dJ4iOU3TK0w|800|center}}<br> | |||
{{Box|1=Ausklammern|2=Gemeinsame Faktoren in einer Summe können ausgeklammert werden.<br> | |||
Beispiel:<br> | |||
8x + 12xy<br> | |||
= <span style="color:red">4x</span>⋅2 + <span style="color:red">4x</span>⋅3y<br> | |||
= <span style="color:red">4x</span>⋅(2 + 3y) | |||
|3=Arbeitsmethode}} | |||
{{Box|Übung 8 Ausklammern|Suche in den LearningApps nach gemeinsamen Faktoren der Summenden und klammere diese dann aus.|Üben}} | |||
<div class="grid"> | |||
<div class="width-1-2"> | |||
{{LearningApp|app=p5pcm6z0a20|width=100%|height=600px}}</div> | |||
<div class="width-1-2"> | |||
{{LearningApp|app=p1on72s7319|width=100%|height=600px}}</div> | |||
</div><br /> | |||
{{Box|Zusätzliche Übungen zum Ausklammern (bei Bedarf)|Löse auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/terme-vereinfachen.shtml '''Aufgabenfuchs'''] die Aufgaben | |||
* 50 | |||
* 51 | |||
* 52|Üben}}<br> | |||
Version vom 14. September 2025, 08:13 Uhr
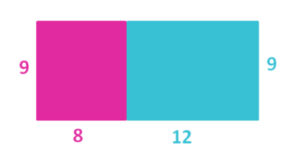
Flächeninhalte mit Termen beschreiben
1. Ausmultiplizieren und Ausklammern (• vor der Klammer )
Vergleiche deine Ideen mit denen im nachfolgenden Video:
Wie lautet der Name dieses Gesetzes? Notiere dies als Überschrift über die obige Zeichnung in dein Heft.
Dieses Gesetz wird im folgenden GeoGebra-Applet noch einmal veranschaulicht. Du kannst die Zahlen durch Variablen ersetzen, indem du die Häkchen "Variable anzeigen" auswählst.
Originallink: https://www.geogebra.org/m/XcFmnc9X

Applet von Birgit Lachner
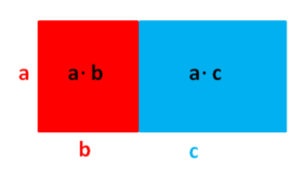
Das Verteilungsgesetz lässt sich auf das Rechnen mit Variablen und Termen übertragen:
Auch hier ist das große Rechteck aus den kleinen Flächen zusammengesetzt. Der Flächeninhalt kann auf zwei Arten angegeben werden:
als Produkt der Seitenlängen a ⋅ ⟨b+c⟩ und als Summe der einzelnen Flächen a⋅b + a⋅c
Es gilt also: a⋅(b+c) = a⋅b + a⋅c.
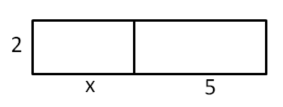
1.1 Ausmultiplizieren
Durch Ausmultiplizieren wird ein Produkt in eine Summe umgewandelt, die Klammern werden also aufgelöst.
Beispiele:
1.2 Ausklammern
Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt.
Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.