Benutzer:Buss-Haskert/Projekt Mein Traumzimmer/Bodenbelag: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 18: | Zeile 18: | ||
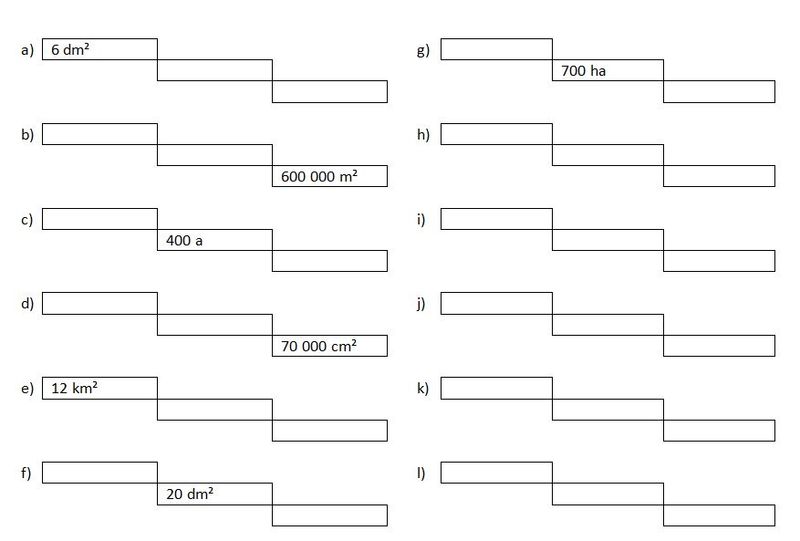
{{Box|Flächenmaße zuordnen|Ordne in den nachfolgenden LearningApps und im GeoGebra-Applet die Flächenmaße passend zu.|Üben}} | {{Box|Flächenmaße zuordnen|Ordne in den nachfolgenden LearningApps und im GeoGebra-Applet die Flächenmaße passend zu.|Üben}} | ||
{{LearningApp|app=1125261|width= | {{LearningApp|app=1125261|width=86%|heigth=600px}} | ||
{{LearningApp|app=pmi7kvng220|width= | {{LearningApp|app=pmi7kvng220|width=86%|height=600px}} | ||
<ggb_applet id="yekpav2e" width=" | Originallink https://www.geogebra.org/m/pvy25pcd<br> | ||
Applet des FLINK-Teams | <ggb_applet id="yekpav2e" width="860" height="414" border="888888" /> | ||
<small>Applet des FLINK-Teams </small> | |||
{{Box|Flächeneinheiten zuordnen|Löse die Aufgaben aus dem Buch. Notiere vollständig. | {{Box|Flächeneinheiten zuordnen|Löse die Aufgaben aus dem Buch. Notiere vollständig. | ||
* S.81, Nr. 1 | * S.81, Nr. 1 | ||
* S.81, Nr. 2|Üben}} | * S.81, Nr. 2|Üben}} | ||
{{Lösung versteckt|1=Kontrolliere deine Lösungen mithilfe der LearninApp:<br> | {{Lösung versteckt|1=Kontrolliere deine Lösungen mithilfe der LearninApp:<br> | ||
{{LearningApp|app=p0u8wndkc23|width=80%|height=600px}}|2=Hilfe zu Nr. 1|3=Verbergen}} | {{LearningApp|app=p0u8wndkc23|width=80%|height=600px}}|2=Hilfe zu Nr. 1|3=Verbergen}} | ||
| Zeile 43: | Zeile 43: | ||
<br> | <br> | ||
{{Box|Flächeneinheiten umwandeln|Ziehe die Fläche in ein anderes Feld. Was beobachtest du?|Meinung}} | {{Box|Flächeneinheiten umwandeln|Ziehe die Fläche in ein anderes Feld. Was beobachtest du?|Meinung}} | ||
Originallink https://www.geogebra.org/m/cbw6ruke<br> | |||
<ggb_applet id="cbw6ruke" width="1052" height="574" border="888888" /> | <ggb_applet id="cbw6ruke" width="1052" height="574" border="888888" /> | ||
Applet des FLINK-Teams | <small>Applet des FLINK-Teams </small> | ||
<br> | <br> | ||
| Zeile 54: | Zeile 55: | ||
1100 mm² = 11 cm²|3=Arbeitsmethode}}<br> | 1100 mm² = 11 cm²|3=Arbeitsmethode}}<br> | ||
{{#ev:youtube|0tk2CoOfHZE| | {{#ev:youtube|0tk2CoOfHZE|860|center}} | ||
| Zeile 61: | Zeile 62: | ||
[[Datei:Treppenspiel Aufgaben.jpg|rahmenlos|800x800px]] | [[Datei:Treppenspiel Aufgaben.jpg|rahmenlos|800x800px]] | ||
Wenn ihr fertig seid, kontrolliert beim Hereinkommen eure Lösungen mit der Musterlösung.|Unterrichtsidee}} | Wenn ihr fertig seid, kontrolliert beim Hereinkommen eure Lösungen mit der Musterlösung.|Unterrichtsidee}} | ||
{{Lösung versteckt|....NOCH ERGÄNZEN|Hilfe|Verbergen}} | {{Lösung versteckt|....NOCH ERGÄNZEN|Hilfe|Verbergen}} | ||
| Zeile 77: | Zeile 77: | ||
*S.81, Nr. 5 | *S.81, Nr. 5 | ||
*S.81, Nr. 6|Üben}} | *S.81, Nr. 6|Üben}} | ||
{{Lösung versteckt|1=Nr. 3a) 24m² = 24·100dm² = 2400dm², denn 1m² = 100dm²<br> | {{Lösung versteckt|1=Nr. 3a) 24m² = 24·100dm² = 2400dm², denn 1m² = 100dm²<br> | ||
Löse die weiteren Aufgaben ebenso.|2=Hilfe zu Nr. 3|3=Verbergen}} | Löse die weiteren Aufgaben ebenso.|2=Hilfe zu Nr. 3|3=Verbergen}} | ||
| Zeile 85: | Zeile 84: | ||
Löse die weiteren Aufgaben ebenso.|2=Hilfe zu Nr. 5|3=Verbergen}} | Löse die weiteren Aufgaben ebenso.|2=Hilfe zu Nr. 5|3=Verbergen}} | ||
{{LearningApp|app=pt2hwuaac21|width= | {{LearningApp|app=pt2hwuaac21|width=86%|height=400px}} | ||
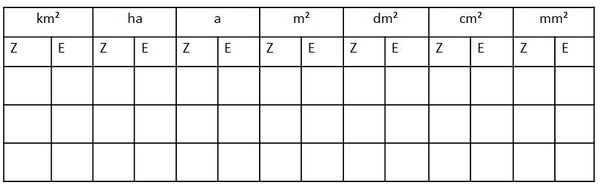
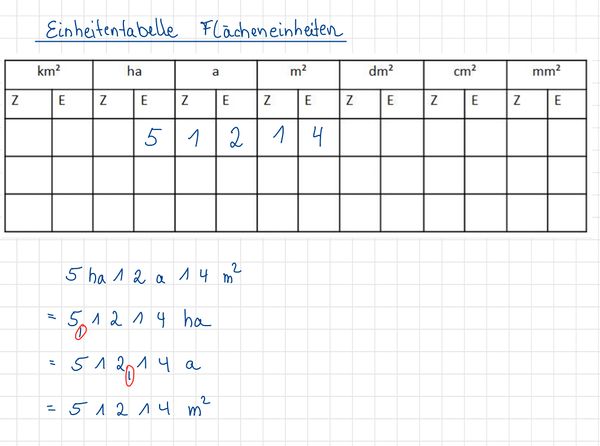
{{Box|Flächeneinheiten - Einheitentabelle|[[Datei:Outdoor-pool-4663122 1920.jpg|rechts|rahmenlos]]Das riesige Außengelände des Freibades hat folgenden Flächeninhalt:<br> | {{Box|Flächeneinheiten - Einheitentabelle|[[Datei:Outdoor-pool-4663122 1920.jpg|rechts|rahmenlos]]Das riesige Außengelände des Freibades hat folgenden Flächeninhalt:<br> | ||
| Zeile 96: | Zeile 95: | ||
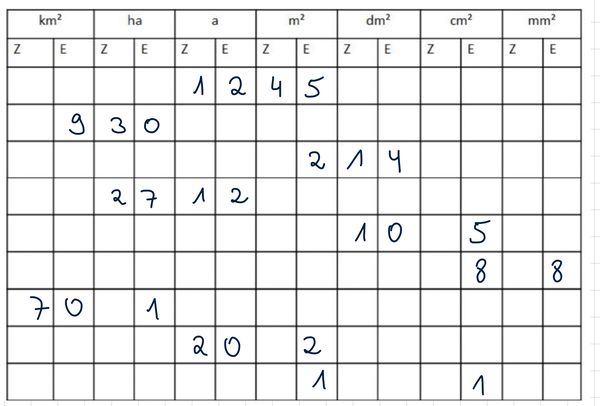
{{Box|Flächen in die Einheitentabelle eintragen|Schiebe den Regler in den nachfolgenden Applets und erkläre, wie die Flächen in die Einheitentabelle eingetragen werden.|Meinung}} | {{Box|Flächen in die Einheitentabelle eintragen|Schiebe den Regler in den nachfolgenden Applets und erkläre, wie die Flächen in die Einheitentabelle eingetragen werden.|Meinung}} | ||
Originallink https://www.geogebra.org/m/cntgvm9k<br> | |||
<ggb_applet id="huy6eff4" width="953" height="500" border="888888" /> | <ggb_applet id="huy6eff4" width="953" height="500" border="888888" /> | ||
Applet des FLINK-Teams Originallink https://www.geogebra.org/m/ | <small>Applet des FLINK-Teams | ||
<br> | <br></small> | ||
Originallink https://www.geogebra.org/m/wgvcpv58<br> | |||
<ggb_applet id="shpemyvd" width="955" height="500" border="888888" /> | <ggb_applet id="shpemyvd" width="955" height="500" border="888888" /> | ||
Applet des FLINK-Teams | <small>Applet des FLINK-Teams </small> | ||
<br> | <br> | ||
Originallink https://www.geogebra.org/m/ahjjmydh<br> | |||
<ggb_applet id="r26z2ehy" width="970" height="499" border="888888" /> | <ggb_applet id="r26z2ehy" width="970" height="499" border="888888" /> | ||
Applet des FLINKE-Teams | <small>Applet des FLINKE-Teams </small> | ||
<br> | <br> | ||
{{LearningApp|app=pypqkyaa320|width=100%|heigth=600px}} | {{LearningApp|app=pypqkyaa320|width=100%|heigth=600px}} | ||
| Zeile 118: | Zeile 120: | ||
*S.82, Nr. 9 | *S.82, Nr. 9 | ||
*S.82, Nr. 10|Üben}} | *S.82, Nr. 10|Üben}} | ||
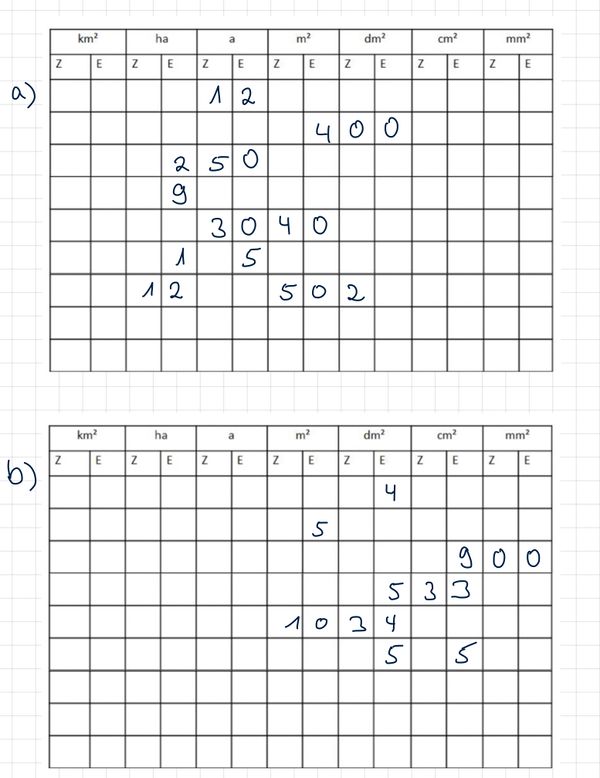
{{Lösung versteckt|[[Datei:SP6 S.82 Nr.9 Tipp.jpg|rahmenlos|600x600px]]|Hilfe zu Nr. 9 (Tabelle)|Verbergen}} | {{Lösung versteckt|[[Datei:SP6 S.82 Nr.9 Tipp.jpg|rahmenlos|600x600px]]|Hilfe zu Nr. 9 (Tabelle)|Verbergen}} | ||
{{Lösung versteckt|[[Datei:SP6 S.82 Nr. 10 (Tipp).jpg|rahmenlos|778x778px]]|Hilfe zu Nr. 10 (Tabelle)|Verbergen}} | {{Lösung versteckt|[[Datei:SP6 S.82 Nr. 10 (Tipp).jpg|rahmenlos|778x778px]]|Hilfe zu Nr. 10 (Tabelle)|Verbergen}} | ||
| Zeile 129: | Zeile 130: | ||
{{Box|Übung 10|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und löse. | {{Box|Übung 10|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und löse. | ||
*S.82, Nr. 15|Üben}} | *S.82, Nr. 15|Üben}} | ||
{{Lösung versteckt|1=Wandle die Ausgangsgröße in die zu ergänzende Größe um:<br> | {{Lösung versteckt|1=Wandle die Ausgangsgröße in die zu ergänzende Größe um:<br> | ||
1m² = 100dm²; 100dm² - 90dm² = 10dm²<br> | 1m² = 100dm²; 100dm² - 90dm² = 10dm²<br> | ||
| Zeile 137: | Zeile 137: | ||
===Rechnen mit Flächeninhalten=== | ===Rechnen mit Flächeninhalten=== | ||
{{LearningApp|app=pch3sbk5t20|width=100%|heigth=600px}} | {{LearningApp|app=pch3sbk5t20|width=100%|heigth=600px}} | ||
{{LearningApp|app=pp1wqfc5a20|width=100%|heigth=600px}} | {{LearningApp|app=pp1wqfc5a20|width=100%|heigth=600px}} | ||
| Zeile 159: | Zeile 144: | ||
* S.82, Nr. 12 | * S.82, Nr. 12 | ||
* S.82, Nr. 13|Üben}} | * S.82, Nr. 13|Üben}} | ||
{{Lösung versteckt|1=Wandle jeweils in die kleinere Einheit um. Umwandlungszahl bei Flächeninhalten: 100! Addiere bzw. subtrahiere danach.<br> | {{Lösung versteckt|1=Wandle jeweils in die kleinere Einheit um. Umwandlungszahl bei Flächeninhalten: 100! Addiere bzw. subtrahiere danach.<br> | ||
Erinnerung: 100 dm² = 1m² (Plakat im Klassenraum)<br> | Erinnerung: 100 dm² = 1m² (Plakat im Klassenraum)<br> | ||
Version vom 25. April 2025, 13:29 Uhr
3. Fußbodenbelag und Deckenfarbe
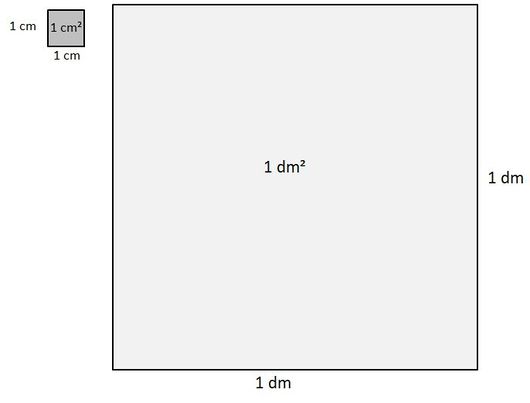
Flächeneinheiten kennenlernen
Originallink https://www.geogebra.org/m/pvy25pcd

Applet des FLINK-Teams
Kontrolliere deine Lösungen mithilfe der LearninApp:
Kontrolliere deine Lösungen mithilfe der LearninApp:
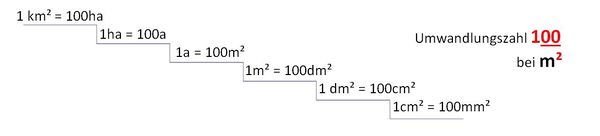
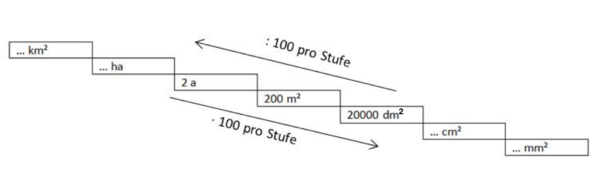
Flächeneinheiten umwandeln
Klicke auf das Bild: Was beobachtest du?


Originallink https://www.geogebra.org/m/cbw6ruke

Applet des FLINK-Teams
Nr. 3a) 24m² = 24·100dm² = 2400dm², denn 1m² = 100dm²
Nr. 4a)500cm² = 500:100dm² = 5dm², denn 100cm²=1dm²
Nr. 5a) 70000cm² = 700dm² = 7m², denn 100cm² = 1dm² und 100dm² = 1m²
Originallink https://www.geogebra.org/m/cntgvm9k

Applet des FLINK-Teams
Originallink https://www.geogebra.org/m/wgvcpv58

Applet des FLINK-Teams
Originallink https://www.geogebra.org/m/ahjjmydh

Applet des FLINKE-Teams
Vermischte Übungen:
Wandle die Ausgangsgröße in die zu ergänzende Größe um:
1m² = 100dm²; 100dm² - 90dm² = 10dm²
1m² = 10000cm²; 10000cm² - 200cm² = ...
Rechnen mit Flächeninhalten
Wandle jeweils in die kleinere Einheit um. Umwandlungszahl bei Flächeninhalten: 100! Addiere bzw. subtrahiere danach.
Erinnerung: 100 dm² = 1m² (Plakat im Klassenraum)
a) 5dm² = 500cm²; 3a = 300 m²
b) 7,2 dm² = 720cm²; 61,3 ha = 6130a
Wandle in die nächstkleinere Einheit um, damit du die Flächen ohne Komma schreiben kannst.
Umwandlungszahl bei Flächeninhalten: 100! Multipliziere bzw. Dividiere anschließend.
Erinnerung: 100 dm² = 1m² (Plakat im Klassenraum)
Wiederholung schriftlich multiplizieren und dividieren:
Flächeneinheiten runden
34,45 m² ≈ 34 m²; 19,38 a ≈ 19 a; 15,87 m² ≈ 16m²