Benutzer:Buss-Haskert/Exponentialfunktion/Exponentialfunktion: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (19 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | [[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]]{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
{{Navigation|[[Benutzer:Buss-Haskert/Exponentialfunktion|Vorwissen]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Wachstum| 1) Lineares und exponentielles Wachstum (Einstieg)]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Wachstum|2) Wachstumsrate und Wachstumsfaktor ]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum|3) Exponentielles Wachstum]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Exponentialfunktion|4) Die Exponentialfunktion]]}} | {{Navigation|[[Benutzer:Buss-Haskert/Exponentialfunktion|Vorwissen]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Wachstum| 1) Lineares und exponentielles Wachstum (Einstieg)]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Wachstum|2) Wachstumsrate und Wachstumsfaktor ]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/exponentielles Wachstum|3) Exponentielles Wachstum]]<br>[[Benutzer:Buss-Haskert/Exponentialfunktion/Exponentialfunktion|4) Die Exponentialfunktion]]}} | ||
<br> | <br> | ||
| Zeile 9: | Zeile 8: | ||
{{Box|1=Exponentialfunktion|2=Die Funktion mit der Gleichung f(x) = c∙a<sup>x</sup> heißt Exponentialfunktion.<br>|3=Arbeitsmethode}} | {{Box|1=Exponentialfunktion|2=Die Funktion mit der Gleichung f(x) = c∙a<sup>x</sup> heißt Exponentialfunktion.<br>|3=Arbeitsmethode}} | ||
{{Box|1=Eigenschaften der Exponentialfunktion|2=Beschreibe die Eigenschaften der Exponentialfunktion f(x) = c∙a< | {{Box|1=Eigenschaften der Exponentialfunktion|2=Beschreibe die Eigenschaften der Exponentialfunktion f(x) = c∙a<sup>x</sup>.<br> | ||
Wähle zunächst c=1. Wie verläuft der Graph der Funktion? Löse den Lückentext und übertrage ihn in dein Heft.|3=Üben}} | Wähle zunächst c=1. Wie verläuft der Graph der Funktion? Löse den Lückentext und übertrage ihn in dein Heft.|3=Üben}} | ||
Originallink https://www.geogebra.org/m/m2gj2nux | |||
<ggb_applet id="m2gj2nux" width="859" height="560" border="888888" /> | <ggb_applet id="m2gj2nux" width="859" height="560" border="888888" /> | ||
Applet von C. Buss-Haskert | Applet von C. Buss-Haskert | ||
{{Box|1=Eigenschaften der Exponentialfunktion|2= | {{Box|1=Eigenschaften der Exponentialfunktion|2= Beschreibe den Verlauf des Graphen der Exponentialfunktion f(x) = a<sup>x</sup>. | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Der Graph verläuft immer '''oberhalb''' der x-Achse.<br> | Der Graph verläuft immer '''oberhalb''' der x-Achse.<br> | ||
Der Graph geht immer durch den Punkt '''⟨0|1⟩''' | Der Graph geht immer durch den Punkt '''⟨0|1⟩'''<br> | ||
Für a>1 '''steigt''' der Graph (Zunahme),<br> | Für a>1 '''steigt''' der Graph (Zunahme),<br> | ||
für 0<a<1 '''fällt''' der Graph (Abnahme).</div>|3=Arbeitsmethode}} | für 0<a<1 '''fällt''' der Graph (Abnahme).</div>|3=Arbeitsmethode}} | ||
{{LearningApp|app=p9z9zf61c25|width=100%|height=600px}} | |||
{{LearningApp|app=pr3f4hnza22|width=100%|height=600px}} | |||
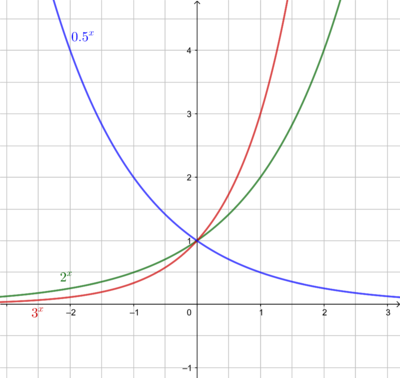
{{Box|1=Wertetabelle und Graph|2=Erstelle je eine Wertetabelle für die Exponentialfunktionen f(x) = 2<sup>x</sup>, f(x) = 3<sup>x</sup> und f(x) = 0,5<sup>x</sup> und zeichne die Graphen in dein Heft.<br> | {{Box|1=Wertetabelle und Graph|2=Erstelle je eine Wertetabelle für die Exponentialfunktionen f(x) = 2<sup>x</sup>, f(x) = 3<sup>x</sup> und f(x) = 0,5<sup>x</sup> und zeichne die Graphen in dein Heft.<br> | ||
[[Datei:Exponentialfunktionen Beispiele.png|rechts|rahmenlos|400x400px]] | [[Datei:Exponentialfunktionen Beispiele.png|rechts|rahmenlos|400x400px]] | ||
{{(!}} class=wikitable | {{(!}} class=wikitable style="width:auto;" | ||
{{!-}} | {{!-}} | ||
{{!}} x | {{!}} x | ||
| Zeile 74: | Zeile 77: | ||
{{Box|Übung 1 - Die Exponentialfunktion|Bearbeite die nachfolgenden LearningApps.|Üben}} | {{Box|Übung 1 - Die Exponentialfunktion|Bearbeite die nachfolgenden LearningApps.|Üben}} | ||
{{LearningApp|app=pj4c5kofa25|width=100%|height=600px}} | |||
{{LearningApp|app=17742628|width=100%|height=600px}} | {{LearningApp|app=17742628|width=100%|height=600px}} | ||
{{LearningApp|app=17853857|width=100%|height=600px}} | {{LearningApp|app=17853857|width=100%|height=600px}} | ||
{{LearningApp|app=pbsfjx6bn22|width=100%|height=800px}} | |||
{{Box|Übung 2|Ordne auf der Seite realmath den Graphen die passende Funktionsgleichung zu. | {{Box|Übung 2|Ordne auf der Seite realmath den Graphen die passende Funktionsgleichung zu. | ||
| Zeile 83: | Zeile 87: | ||
{{Box|1=Spiegelung an der y-Achse|2=Zeichne mit [https://www.geogebra.org/classic#graphing GeoGebra] den Funktionsgraphen zu f(x) = 2<sup>x</sup> und spiegele den Graphen an der y-Achse. Wie lautet die Gleichung der gespiegelten Funktion? Was fällt dir auf?|3=Frage}} | {{Box|1=Spiegelung an der y-Achse|2=Zeichne mit [https://www.geogebra.org/classic#graphing GeoGebra] den Funktionsgraphen zu f(x) = 2<sup>x</sup> und spiegele den Graphen an der y-Achse. Wie lautet die Gleichung der gespiegelten Funktion? Was fällt dir auf?|3=Frage}} | ||
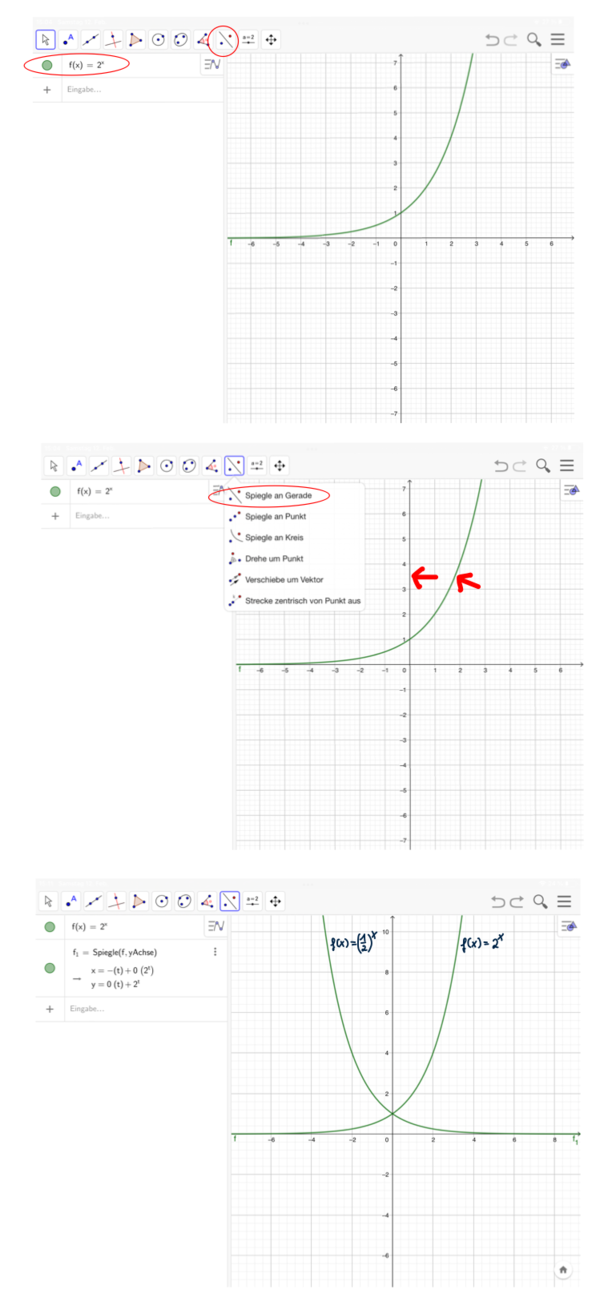
{{Lösung versteckt|Die Bilderfolge zeigt dir, wie du in GeoGebra Funktionsgraphen an Geraden spiegelst. Wähle das entsprechende Werkzeug und berühre anschließend den Graphen und die y-Achse (rote Pfeile). | |||
[[Datei:Exponentialfunktion an der y-Achse spiegeln GeoGebra.png|rahmenlos|1310x1310px]]|Wie kann ich in GeoGebra den Funktionsgraphen an der y-Achse spiegeln?|Verbergen}} | |||
===Die Exponentialfunktion und Corona=== | ===Die Exponentialfunktion und Corona=== | ||
{{#ev:youtube|eOhQtMYcGP8|800|center}} | {{#ev:youtube|eOhQtMYcGP8|800|center}} | ||
Aktuelle Version vom 10. Januar 2025, 09:39 Uhr
Vorwissen
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
4) Die Exponentialfunktion
1) Lineares und exponentielles Wachstum (Einstieg)
2) Wachstumsrate und Wachstumsfaktor
3) Exponentielles Wachstum
4) Die Exponentialfunktion
4 Die Exponentialfunktion
Originallink https://www.geogebra.org/m/m2gj2nux

Applet von C. Buss-Haskert
Die Bilderfolge zeigt dir, wie du in GeoGebra Funktionsgraphen an Geraden spiegelst. Wähle das entsprechende Werkzeug und berühre anschließend den Graphen und die y-Achse (rote Pfeile).