Geometrie im Dreieck/Mehr als eine Linie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierungen: Manuelle Zurücksetzung 2017-Quelltext-Bearbeitung |
||
| (30 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== | ==Information== | ||
Falls du dich bei diesem Thema nicht mehr sicher fühlst und lieber zu Beginn oder zwischendurch dein Vorwissen auffrischen möchtest, kannst du dafür in deinem Mathebuch die Zusammenfassung des Kapitels 2 auf S. 70 verwenden und darüber hinaus folgende Seiten: | {{Box | ||
|1=|2= In diesem Lernpfadkapitel werden besondere Linien eines Dreiecks behandelt. | |||
Bei diesen Linien handelt es sich um die '''Mittelsenkrechte''', die '''Winkelhalbierende''' und die '''Seitenhalbierende'''. Falls du dich bei diesem Thema nicht mehr sicher fühlst und lieber zu Beginn oder zwischendurch dein Vorwissen auffrischen möchtest, kannst du dafür in deinem Mathebuch (Dreifachmathe, Klasse 8) die Zusammenfassung des Kapitels 2 auf S. 70 verwenden und darüber hinaus folgende Seiten: | |||
Mittelsenkrechte - S. 56 | Mittelsenkrechte - S. 56 | ||
| Zeile 8: | Zeile 11: | ||
Seitenhalbierende - S. 64 | Seitenhalbierende - S. 64 | ||
== | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
* Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gekennzeichnet sind, haben eine '''geringe Schwierigkeit'''. | |||
* Aufgaben, die '''<span style="color: #CD2990">pink</span>''' gekennzeichnet sind, haben eine '''mittlere Schwierigkeit'''. | |||
* Aufgaben, die '''<span style="color: #5E43A5">lila</span>''' gekennzeichnet sind, haben eine '''hohe Schwierigkeit'''. | |||
Viel Erfolg! | |||
|3=Kurzinfo}} | |||
==Martins und Marias Problem== | |||
[[Datei:Marias Zeichnung.png|mini|Marias Zeichnung]] | [[Datei:Marias Zeichnung.png|mini|Marias Zeichnung]] | ||
{{Box|Denk nach!|Martin und Maria sollen als Hausaufgabe in ein gleichseitiges Dreieck die Mittelsenkrechten, die Winkelhalbierenden und die Seitenhalbierenden einzeichnen. Maria behauptet, sie hätte alle Linien eingezeichnet. Martin meint, sie hätte die Mittelsenkrechten und die Seitenhalbierenden vergessen. Was meinst du? Begründe deine Antwort. Schreibe auf das Arbeitsblatt und vergleiche abschließend mit den Eigenschaften in der ersten Aufgabe. |Arbeitsmethode| Farbe={{Farbe|grau}} }} | {{Box|Denk nach!| | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Arbeitsblatt''' | |||
Martin und Maria sollen als Hausaufgabe in ein gleichseitiges Dreieck die Mittelsenkrechten, die Winkelhalbierenden und die Seitenhalbierenden einzeichnen. Maria behauptet, sie hätte alle Linien eingezeichnet. Martin meint, sie hätte die Mittelsenkrechten und die Seitenhalbierenden vergessen. Was meinst du? Begründe deine Antwort. Schreibe auf das Arbeitsblatt und vergleiche abschließend mit den Eigenschaften in der ersten Aufgabe. | |||
|Arbeitsmethode| Farbe={{Farbe|grau}} }} | |||
| Zeile 16: | Zeile 34: | ||
== | ==Eigenschaften der besonderen Linien== | ||
{{Box|Aufgabe 1| Ordne die Aussagen den Linien zu. Sichere das Ergebnis mit einem Screenshot. | {{Box|Aufgabe 1: Eigenschaften zuordnen|Ordne die Aussagen den Linien zu. Sichere das Ergebnis mit einem Screenshot. | ||
Hinweis: Falls dein Ergebnis als 'nicht richtig' angezeigt wird, kannst du versuchen Karten, die doppelt vorkommen, zu vertauschen. | |||
{{LearningApp|app=pj8oiu93a24|width=100%|height=400px}}|Arbeitsmethode| Farbe={{Farbe|grau}} }} | {{LearningApp|app=pj8oiu93a24|width=100%|height=400px}}|Arbeitsmethode| Farbe={{Farbe|grau}} }} | ||
== | ==Konstruktion 1== | ||
In dieser Aufgabe geht es darum, zu üben, die besonderen Linien des Dreiecks selbst zu konstruieren. Wähle eines der Level aus. | In dieser Aufgabe geht es darum, zu üben, die besonderen Linien des Dreiecks selbst zu konstruieren. Wähle eines der Level aus. | ||
{{Box|Level 1|{{Lösung versteckt | | {{Box|Aufgabe 2: Besondere Linien konstruieren - Level 1|{{Lösung versteckt | | ||
Fülle die Lücken des folgenden Textes, indem du das richtige Wort aus den Vorschlägen auswählst. Sichere dein Ergebnis mit einem Screenshot. | Fülle die Lücken des folgenden Textes, indem du das richtige Wort aus den Vorschlägen auswählst. Sichere dein Ergebnis mit einem Screenshot. | ||
| Zeile 34: | Zeile 52: | ||
{{Box|Level 2|{{Lösung versteckt | | {{Box|Aufgabe 2: Besondere Linien konstruieren - Level 2|{{Lösung versteckt | | ||
Fülle die Lücken des folgenden Textes. Sichere dein Ergebnis mit einem Screenshot. | Fülle die Lücken des folgenden Textes. Sichere dein Ergebnis mit einem Screenshot. | ||
{{LearningApp|app=p77ndiean24|width=100%|height=400px}} | {{LearningApp|app=p77ndiean24|width=100%|height=400px}} | ||
| Zeile 40: | Zeile 58: | ||
{{Box|Level 3|{{Lösung versteckt | | {{Box|Aufgabe 2: Besondere Linien konstruieren - Level 3|{{Lösung versteckt | | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Arbeitsblatt''' | |||
Beschreibe in eigenen Worten auf dem Arbeitsblatt, wie du die folgenden Linien mit dem Zirkel konstruieren kannst: | Beschreibe in eigenen Worten auf dem Arbeitsblatt, wie du die folgenden Linien mit dem Zirkel konstruieren kannst: | ||
| Zeile 89: | Zeile 109: | ||
== | ==Konstruktion 2== | ||
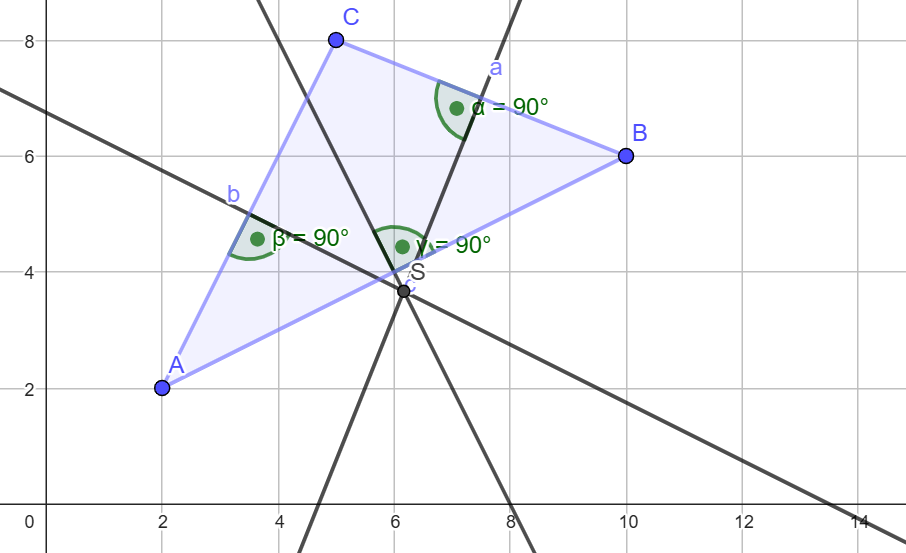
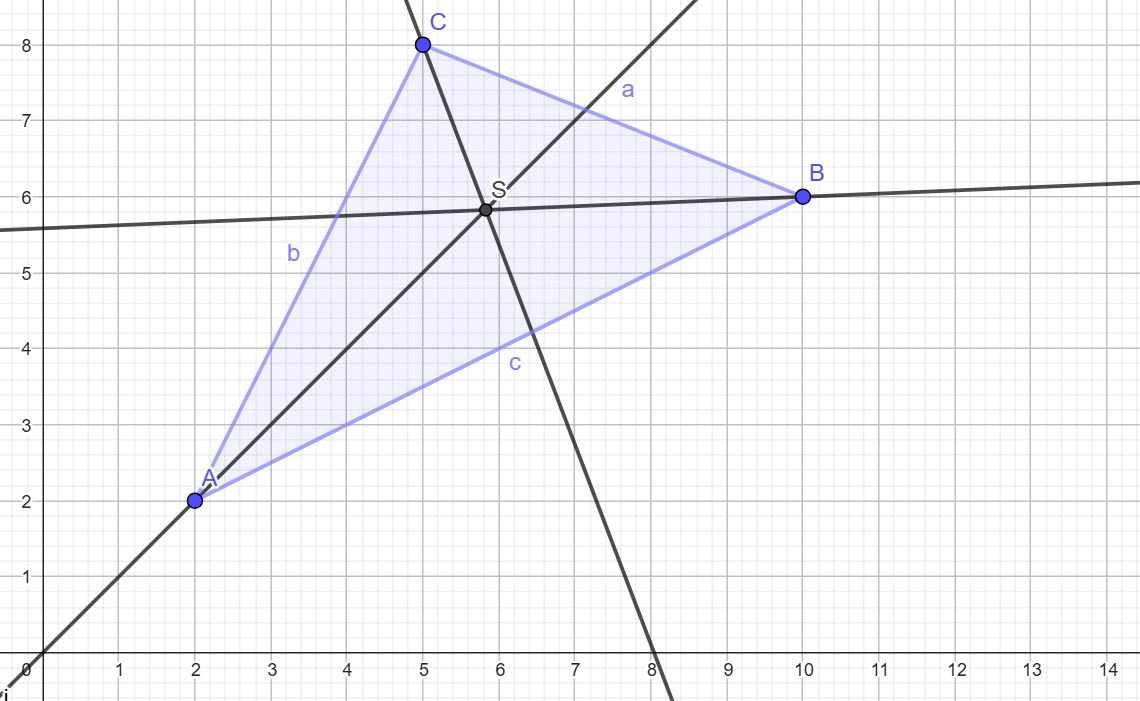
{{Box|Aufgabe 3|Konstruiere folgende Linien mit Geodreieck oder Zirkel. Nutze dafür das Arbeitsblatt. | {{Box|Aufgabe 3: Besondere Linien konstruieren 2| | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Arbeitsblatt''' | |||
Konstruiere folgende Linien mit Geodreieck oder Zirkel. Nutze dafür das Arbeitsblatt. | |||
[[Datei:Image 2.png]] | [[Datei:Image 2.png]] | ||
| Zeile 115: | Zeile 138: | ||
|Arbeitsmethode| Farbe={{Farbe|grau}} }} | |Arbeitsmethode| Farbe={{Farbe|grau}} }} | ||
== | ==Hochseilgarten== | ||
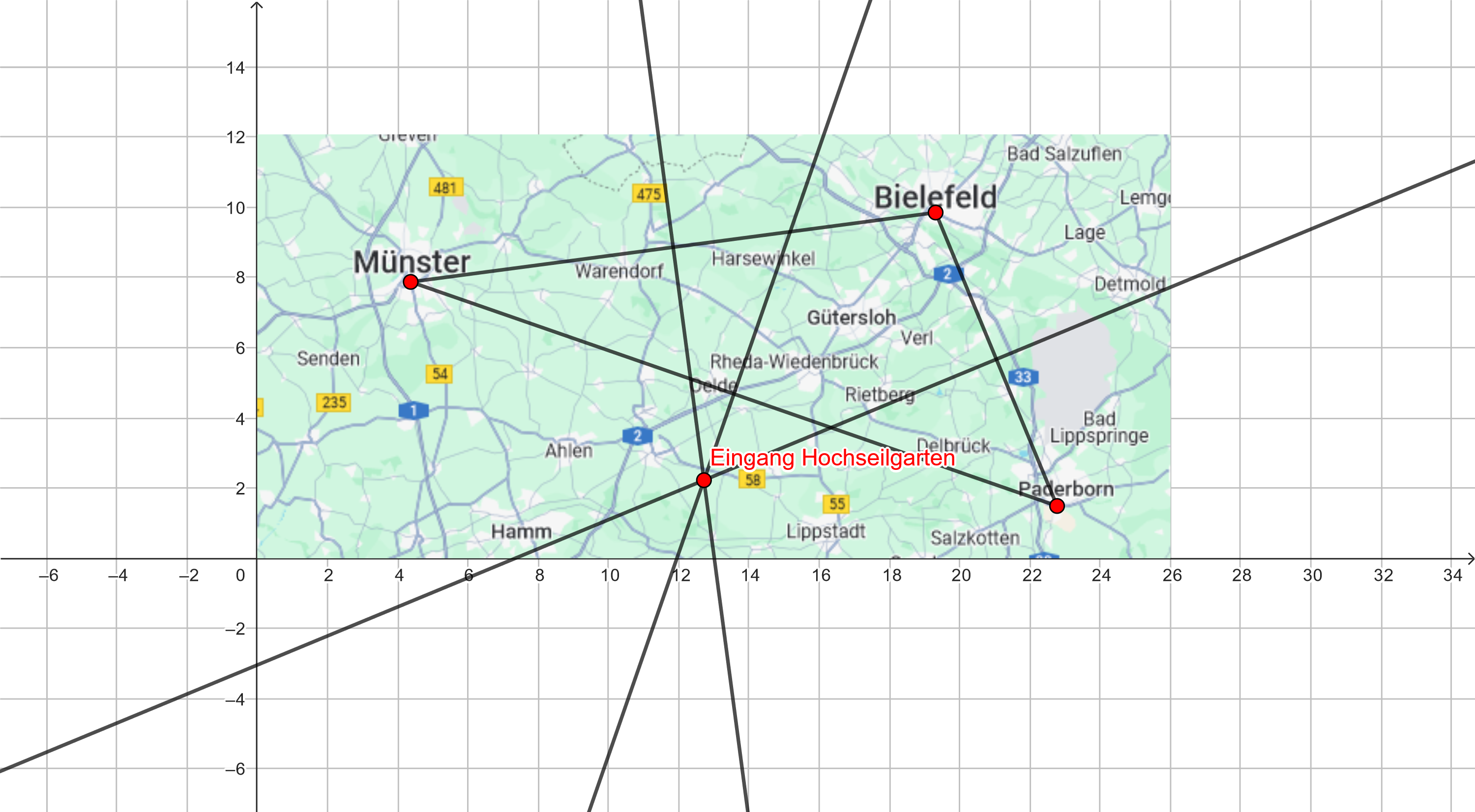
{{Box|Aufgabe 4|Die drei Städte Münster, Bielefeld und Paderborn möchten zusammen einen Hochseilgarten bauen. Der Eingang vom Hochseilgarten soll von allen drei Städten gleich weit entfernt sein. | {{Box|Aufgabe 4: Anwendungsaufgabe|Die drei Städte Münster, Bielefeld und Paderborn möchten zusammen einen Hochseilgarten bauen. Der Eingang vom Hochseilgarten soll von allen drei Städten gleich weit entfernt sein. | ||
a) Bestimme die Koordinaten des Eingangs. Nutze zur Bestimmung der Koordinaten des Eingangs | a) Bestimme die Koordinaten des Eingangs. Nutze zur Bestimmung der Koordinaten des Eingangs das folgende GeoGebra-Applet. Runde auf die zweite Nachkommastelle. | ||
<ggb_applet id="fekpys28" width="950" height="520" /> | |||
{{Lösung versteckt|Überlege, welche der drei besonderen Linien im Dreieck den gleichen Abstand zu den Eckpunkten hat. | 1. Tipp anzeigen | 1. Tipp verbergen}} | {{Lösung versteckt|Überlege, welche der drei besonderen Linien im Dreieck den gleichen Abstand zu den Eckpunkten hat. | 1. Tipp anzeigen | 1. Tipp verbergen}} | ||
| Zeile 125: | Zeile 149: | ||
{{Lösung versteckt|[[Datei:Textaufgabe Hochseilgarten Lösung.png|Lösung]]. Also muss der Eingang vom Hochseilgarten im Punkt S(12,72; 2,22) liegen.| Lösung anzeigen | Lösung verbergen}} | {{Lösung versteckt|[[Datei:Textaufgabe Hochseilgarten Lösung.png|Lösung]]. Also muss der Eingang vom Hochseilgarten im Punkt S(12,72; 2,22) liegen.| Lösung anzeigen | Lösung verbergen}} | ||
b) Beurteile, ob dies genau so umgesetzt werden könnte und ob dies wirklich der beste Ort für den Eingang ist. | b) Beurteile, ob dies genau so umgesetzt werden könnte und ob dies wirklich der beste Ort für den Eingang ist. | ||
| Zeile 141: | Zeile 166: | ||
|Arbeitsmethode| Farbe={{Farbe|grau}} }} | |Arbeitsmethode| Farbe={{Farbe|grau}} }} | ||
Hier findest du zurück zum Ausgangspunkt der Stunde. | |||
[[Geometrie im Dreieck]] | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Version vom 2. Dezember 2024, 14:34 Uhr
Information
Martins und Marias Problem
Eigenschaften der besonderen Linien
Konstruktion 1
In dieser Aufgabe geht es darum, zu üben, die besonderen Linien des Dreiecks selbst zu konstruieren. Wähle eines der Level aus.
Konstruktion 2
Hochseilgarten
Hier findest du zurück zum Ausgangspunkt der Stunde.
Geometrie im Dreieck