3. Gegenzahl und Betrag
Gegenzahl und Betrag
Zwei Zahlen, die ein entgegengesetztes Vorzeichen, aber zur Null denselben Abstand haben, heißen entgegengesetzte Zahlen oder Gegenzahlen.

Der Abstand einer Zahl zur 0 heißt
Betrag und wird mit Betragsstrichen gekennzeichnet, z.B. |-4| = 4; |+4| = 4.
Übung 2
Löse die LearningApps.
4. Rationale Zahlen addieren
Originallink https://www.geogebra.org/m/mc8MkyHj
Applet von Konrad Maier
Übung 2
Wähle zwei Übungen aus der Sammlung aus.
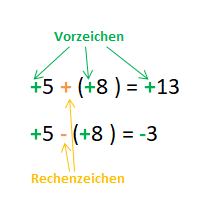
Vorzeichen und Rechenzeichen
Treffen Vorzeichen und Rechenzeichen aufeinander, so wird immer eine Klammer gesetzt. Das Vorzeichen gibt an, ob die Zahl positiv oder negativ ist. Das Rechenzeichen gibt an, ob die Zahlen addiert oder subtrahiert werden.
Rationale Zahlen addieren und subtrahieren
Addieren:
Bei gleichen Vorzeichen addiere die Zahlen ohne ihr Vorzeichen zu berücksichtigen. Das Ergebnis erhält das gemeinsame Vorzeichen.
Bei verschiedenen Vorzeichen subtrahiere ohne das Vorzeichen zu berücksichtigen die Zahl mit dem kleineren Betrag von der größeren. Das Ergebnis erhält das Vorzeichen der Zahl mit dem größeren Betrag.
Subtrahieren:
Subtrahiere eine rationale Zahl, indem du ihre Gegenzahl addierst.
WICHTIG:
Erkläre die Aufgabe immer mithilfe einer Grundvorstellung, z.B. Schulden/Guthaben, Aufzugfahren, Zahlengerade, ...
Die Regeln zum Addieren und Subtrahieren klingen sehr kompliziert. Die Beispiele verdeutlichen die Regeln noch einmal. Hilfreich ist immer, wenn du die Rechnung mithilfe einer Grundvorstellung erklärst!

Alles klar? Dann löse nochmals mindestens 10 Aufgaben. Verdeutliche dir jede Aufgabe mithilfe einer Grundvorstellung und erkläre dann noch einmal die Rechenregeln.
Originallink https://www.geogebra.org/m/FgbWuHw7
Applet von Birgit Lachner
Sprinteraufgabe
Löse Aufgaben zur Addition rationaler Zahlen in der Tabelle unten. Du kannst den Zahlbereich verändern.
Verkürzte Schreibweise
In der verkürzten Schreibweise werden Vor-und Rechenzeichen durch nur ein Rechenzeichen ersetzt:
+(+) = +
+(-) = -
-(+) = -
-(-) = +
Eselsbrücke:
Merke dir diese Regel mit dem Memoryspiel:
Wenn du zwei gleiche Karten aufdeckst, freust du dich (+),
also +(+) = + und -(-) = +
wenn du verschiedene Karten aufdeckst, bist du traurig (-),
also +(-) = - und -(+) = -
So lassen sich Rechnungen viel kürzer schreiben. Erkläre die Rechnung auch weiterhin immer mit einer Grundvorstellung zu den negativen Zahlen.
Beispiel:
(-5) + (+27)
= -5 + 27 "Ich habe 5€ Schulden und bekomme 27€ Taschengeld."
= + 22 "Dann habe ich keine Schulden mehr, sondern (27-5)€ Guthaben."
+16 - (-21) "Ich habe 16€ und mir gebe 21€ Schulden ab."
= 16 + 21 "Ich habe 16€ und bekomme 21€ dazu."
= 37
-48 + (-29)
= -48 - 29 "Ich habe 48€ Schulden und gebe noch einmal 29€ aus."
= -77 "Dann habe ich noch mehr Schulden."
+52 - (+39)
= 52 - 39 "Ich habe 52€ und gebe 39€ aus."
= 13 "Dann habe ich noch 13€."
Die kürzere Schreibweise kannst du dir auch vorstellen mit Höhenmetern. Welche Bedeutung hat dann das Addieren (+) bzw. das Subtrahieren (-)? Erkläre.
Löse mindestens 10 Aufgaben. Auf geht's auf den Leuchtturm:
Übung 5
Löse die nachfolgenden Apps. Schreibe die Aufgabe zunächst ohne Klammern (verkürzte Schreibweise). Erkläre sie danach mit einer Grundvorstellung zu den negativen Zahlen und berechne dann das Ergebnis.
Übung 6
Erfinde jeweils eine Geschichte zu den folgenden Aufgaben und löse dann die Aufgabe.
- a) -8 - 23
- b) -58 + 24
- c) 123 - 150
- d) 25 - 13
Übung 7
Löse die Apps zur Addition von ganzen Zahlen
Übung 8
Löse die Apps zur Subtraktion von ganzen Zahlen
Übung 9
Löse die Aufgabe aus dem Buch
- S. 43, Nr. 1
- S. 43, Nr. 3 (Kontrolliere deine Lösungen mit der LearningApp unten.)
Tipp zu Nr. 1 (Vorstellungen)
a) Vorstellung an der Zahlengeraden: Laufe zunächst 8 Schritte nach rechts (+) und von dort 15 Schritte nach links (-15). Wo kommst du an?
Vorstellung am Thermometer: Das Thermometer steht bei +8°C und die Temperatur sinkt (-) um 15°C. Wie kalt ist es jetzt?
Vorstellung im Parkhaus: Du stehst im 8.OG ((+) Obergeschoss) und fährst 15 Stockwerke nach unten (-).
Vorstellung mit Schulden und Guthaben: Du hast 8€ Guthaben (+) und gibst 15€ aus (-). Dann muss du dir Geld leihen, hast also Schulden.
Übung 10
Löse die Apps zur Subtraktion von ganzen Zahlen