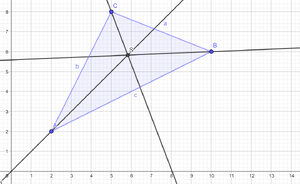
Geometrie im Dreieck/Mehr als eine Linie
Inhaltsverzeichnis
Einstieg
Aufgabe 1: Besondere Linien konstruieren 1
Fülle die Lücken des folgenden Textes, indem du das richtige Wort aus den Vorschlägen auswählst.
Fülle die Lücken des folgenden Textes.
Beschreibe in eigenen Worten, wie du die folgenden Linien mit dem Zirkel konstruieren kannst:
a) Winkelhalbierende
Die folgenden Punkte sollten in deiner Lösung enthalten sein:
- um den Eckpunkt einen Kreis zeichnen
- um die Schnittpunkte des Kreises mit den Schenkeln erneut Kreise zeichnen
- die Schnittpunkte der beiden neuen Kreise mit dem Eckpunkt durch eine Gerade verbinden
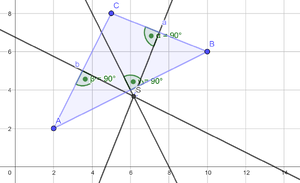
b) Mittelsenkrechte
Die folgenden Punkte sollten in deiner Lösung enthalten sein:
- um beide Eckpunkte einen Kreis einzeichnen
- Kreise müssen den gleichen Radius haben und der Radius muss größer als die halbe Seitenlänge sein
- die Schnittpunkte der beiden Kreise durch eine Gerade verbinden
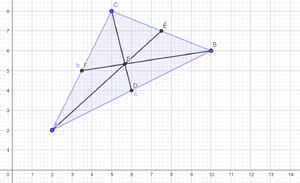
c) Seitenhalbierende
Die folgenden Punkte sollten in deiner Lösung enthalten sein:
- um beide Eckpunkte einen Kreis einzeichnen
- Kreise müssen den gleichen Radius haben und der Radius muss größer als die halbe Seitenlänge sein
- die Schnittpunkte der beiden Kreise durch eine Gerade verbinden; der Schnittpunkt dieser Gerade mit der Seite ist der Mittelpunkt der Seite
- den Mittelpunkt der Seite mit der gegenüberliegenden Ecke durch eine Strecke verbinden
Aufgabe 2: Besondere Linien konstruieren 2
Aufgabe 3: Anwendungsaufgabe
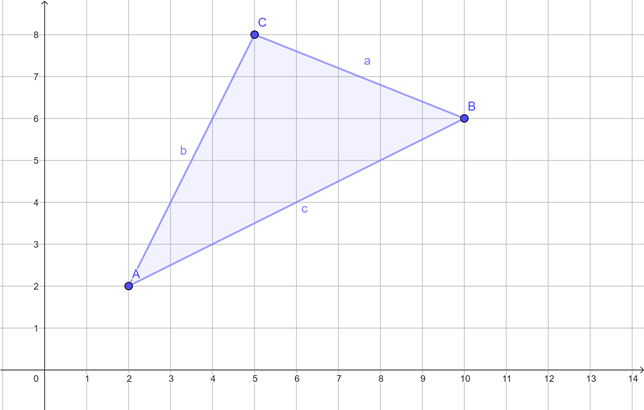
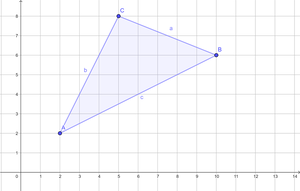
Die drei Städte Münster, Bielefeld und Paderborn möchten zusammen einen Hochseilgarten bauen. Der Eingang vom Hochseilgarten soll von allen drei Städten gleich weit entfernt sein.
a) Bestimme die Koordinaten des Eingangs. Nutze zu Bestimmung der Koordinaten des Eingangs dieses GeoGebra-Applet.
b) Beurteile, ob dieses Modell realitätsnah ist und welche Vereinfachungen du angenommen hast.
Zu beachten sind zum Beispiel folgende Vereinfachungen:
- Der Eingang befindet sich eigentlich nie nur an einem Punkt.
- Eventuell befindet sich an diesem Ort gar keine freie Fläche.
- Die Luftlinie entspricht nicht der tatsächlichen Straßenführung. Es kann also trotzdem unterschiedlich lange Anreisezeiten geben.
- ...
Aufgabe 4: Sicherung