Digitale Werkzeuge in der Schule/Rund ums Dreieck/Winkel im Dreieck: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
|||
| (29 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<br /> | <br /> | ||
{{Box|1=Info|2=In diesem Lernpfadkapitel lernst Eigenschaft | {{Box|1=Info|2=In diesem Lernpfadkapitel lernst du, welche Eigenschaft die Winkel in Dreiecken immer haben. Diese werden wir in einer Regel festhalten und du übst, wie man sie richtig anwendet. | ||
Bei den Aufgaben unterscheiden wir folgende Typen: | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
| Zeile 21: | Zeile 21: | ||
==Erforschung== | ==Erforschung== | ||
Die Winkel in den Dreiecken oben sind also alle | Die Winkel in den Dreiecken oben sind also alle gleich groß. Allerdings waren die Dreiecke oben auch alle gleichseitig. Gibt es trotzdem eine Regel, die sich auf alle Dreiecke anwenden lässt? | ||
In den folgenden Aufgaben wirst du genau das untersuchen und versuchen selbst die Regel herauszufinden, mit der du einen (oder mehrere) Innenwinkel in jedem Dreieck bestimmen kannst ohne jedes Mal nachmessen zu müssen. | In den folgenden Aufgaben wirst du genau das untersuchen und versuchen, selbst die Regel herauszufinden, mit der du einen (oder mehrere) Innenwinkel in jedem Dreieck bestimmen kannst, ohne jedes Mal nachmessen zu müssen. | ||
===Gleichseitige Dreiecke=== | ===Gleichseitige Dreiecke=== | ||
{{Box | Aufgabe 2: Winkel im gleichseitigen Dreieck | | {{Box | Aufgabe 2: Winkel im gleichseitigen Dreieck | | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
Notiere dir auf dem Arbeitsblatt, was mit den Innenwinkeln des Dreiecks passiert, egal wie lang die Seitenlänge des Dreiecks ist. | Notiere dir auf dem Arbeitsblatt, was mit den Innenwinkeln des Dreiecks passiert, egal wie lang die Seitenlänge des Dreiecks ist. | ||
| Zeile 41: | Zeile 42: | ||
{{Box | Aufgabe 3: Winkel im allgemeinen Dreieck |[[Datei:Grundlagen-bearbeiten.png|30px|middle]]'''zurück zum Arbeitsblatt''' | {{Box | Aufgabe 3: Winkel im allgemeinen Dreieck |[[Datei:Grundlagen-bearbeiten.png|30px|middle]]'''zurück zum Arbeitsblatt''' | ||
Erstelle ein beliebiges | Erstelle ein beliebiges Dreieck mit der App. Notiere dir auf dem Arbeitsblatt, welche Eigenschaft die Summe der drei Winkel in einem beliebigen Dreieck hat. Begründe deine Vermutung. Überprüfe anschließend deine Vermutungen durch weitere Dreiecke. | ||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Du kannst das Dreieck an den Ecken in eine beliebige Form ziehen. Klicke danach auf Start und folge den Anweisungen des Applets. | [[Datei:About icon (The Noun Project).svg|15px|middle]] Du kannst das Dreieck an den Ecken in eine beliebige Form ziehen. Klicke danach auf Start und folge den Anweisungen des Applets. | ||
| Zeile 49: | Zeile 49: | ||
{{Box | |||
|1=Info | |||
|2=In diesem Lernpfadkapitel <Kurzbeschreibung des Kapitelziels> | |||
Für die nächste Aufgabe solltest du Kapitel 2: [[Rund ums Dreieck/Winkel an Geraden|Winkel an Geraden]] schon bearbeitet haben und wissen, was Scheitel- und Stufenwinkel sind. Wenn das nicht der Fall ist, kannst du diese Aufgabe einfach überspringen. | Für die nächste Aufgabe solltest du Kapitel 2: [[Rund ums Dreieck/Winkel an Geraden|Winkel an Geraden]] schon bearbeitet haben und wissen, was Scheitel- und Stufenwinkel sind. Wenn das nicht der Fall ist, kannst du diese Aufgabe einfach überspringen. | ||
Wenn du aber schon Kapitel 2 bearbeitet hast, zeigt dir die folgende Forschungsaufgabe noch eine weitere Begründung für die Innenwinkelsumme in Dreiecken ohne die Winkel umständlich verschieben zu müssen, sondern nur mithilfe einer Hilfslinie. Dieser Lösungsweg kann später bei einigen Anwendungsaufgaben sehr nützlich sein! | Wenn du aber schon Kapitel 2 bearbeitet hast, zeigt dir die folgende Forschungsaufgabe noch eine weitere Begründung für die Innenwinkelsumme in Dreiecken ohne die Winkel umständlich verschieben zu müssen, sondern nur mithilfe einer Hilfslinie. Dieser Lösungsweg kann später bei einigen Anwendungsaufgaben sehr nützlich sein! | ||
|3=Kurzinfo}} | |||
<br /> | <br /> | ||
{{Box | Aufgabe 4: Stufen- und Wechselwinkel im Dreieck |[[Datei:Grundlagen-bearbeiten.png|30px|middle]]'''zurück zum Arbeitsblatt''' | {{Box | Aufgabe 4: Stufen- und Wechselwinkel im Dreieck |[[Datei:Grundlagen-bearbeiten.png|30px|middle]]'''zurück zum Arbeitsblatt''' | ||
Ziehe das | Ziehe das Dreieck in beliebige Formen. Notiere dir auf dem Arbeitsblatt, warum die grünen bzw. blauen Winkel immer gleich groß sind. Versuche, die Begriffe Wechselwinkel und Stufenwinkel zu nutzen. Welche Summe ergeben die drei Winkel zusammen? | ||
<ggb_applet id="qbdunxsv" width="1000" height="538" border="888888" /> | Arbeitsmethode | Farbe=#CD2990 }} | <ggb_applet id="qbdunxsv" width="1000" height="538" border="888888" /> | Arbeitsmethode | Farbe=#CD2990 }} | ||
| Zeile 67: | Zeile 67: | ||
==Innenwinkelsumme im Dreieck== | ==Innenwinkelsumme im Dreieck== | ||
{{Box | Merksatz: Der Innenwinkelsummensatz für Dreiecke | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | {{Box | Merksatz: Der Innenwinkelsummensatz für Dreiecke |2=[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
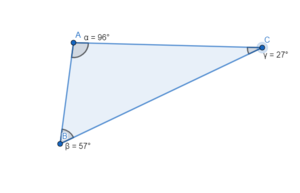
[[Datei:Dreieck_mit_Winkelangaben.png|mini|Auch hier ergeben die drei Winkel insgesamt 180°]] | |||
Notiere dir den Merksatz auf deinem Arbeitsblatt. | Notiere dir den Merksatz auf deinem Arbeitsblatt. | ||
| Zeile 74: | Zeile 74: | ||
<br> | <br> | ||
Für die drei Winkel Alpha, Beta und Gamma gilt also: <br> | Für die drei Winkel Alpha, Beta und Gamma gilt also: <br> | ||
α+β+γ | α+β+γ = 180°. | ||
| Farbe={{Farbe|grün|dunkel}}}} | | Farbe={{Farbe|grün|dunkel}}}} | ||
==Aufgaben== | ==Aufgaben== | ||
Bearbeite nun die untenstehenden Aufgaben. Beginne mit Aufgabe 5. Falls dir die Rechnungen leicht fallen, kannst du auch direkt zu Aufgabe 6 weitergehen. Wenn du Platz brauchst, um deine Rechnungen zu notieren, kannst du hierfür den Platz auf dem Arbeitsblatt nutzen.<br /> | Bearbeite nun die untenstehenden Aufgaben. Beginne mit Aufgabe 5. Falls dir die Rechnungen leicht fallen, kannst du auch direkt zu Aufgabe 6 weitergehen. Wenn du Platz brauchst, um deine Rechnungen zu notieren, kannst du hierfür den Platz auf dem Arbeitsblatt nutzen. | ||
<br /> | |||
{{Box | Aufgabe 5: Ergänze die Tabelle|Wende den Innenwinkelsummensatz an und berechne den fehlenden Winkel. | {{Box | Aufgabe 5: Ergänze die Tabelle|Wende den Innenwinkelsummensatz an und berechne den fehlenden Winkel. | ||
| Zeile 95: | Zeile 98: | ||
{{LearningApp|width=100%|height=500px|app=25228963}} | Arbeitsmethode}} | {{LearningApp|width=100%|height=500px|app=25228963}} | Arbeitsmethode}} | ||
==Knobelaufgabe== | |||
{{Box|1=Aufgabe 8: Das Rutschenproblem |2= [[Datei:Grundlagen-bearbeiten.png|30px|middle]]'''zurück zum Arbeitsblatt''' | |||
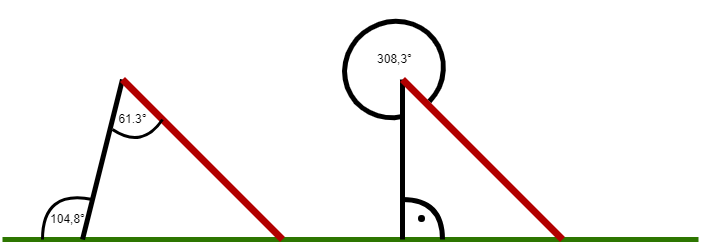
Tim will während der großen Pause rutschen. Tim ist sich jedoch nicht sicher, welche Rutsche steiler sein könnte. Vor der Rutsche befindet sich der Bauplan der beiden Rutschen, wo einige Winkel eingezeichnet sind. Jedoch fehlen einige Angaben. Versuche, Tim zu helfen und bestimme, welche der beiden Rutschen steiler ist. Kreuze die richtige Antwort an. | |||
[[Datei:RutschenAufgabe2.png|mini|800px|Bauplan der Rutschen]] | [[Datei:RutschenAufgabe2.png|mini|800px|Bauplan der Rutschen]] | ||
| Zeile 112: | Zeile 112: | ||
|3= Arbeitsmethode | Farbe=#CD2990 }} | |3= Arbeitsmethode | Farbe=#CD2990 }} | ||
{{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Rund_ums_Dreieck}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Digitale Werkzeuge in der Schule]] | |||
Aktuelle Version vom 2. November 2022, 09:38 Uhr
Muster untersuchen
Erforschung
Die Winkel in den Dreiecken oben sind also alle gleich groß. Allerdings waren die Dreiecke oben auch alle gleichseitig. Gibt es trotzdem eine Regel, die sich auf alle Dreiecke anwenden lässt?
In den folgenden Aufgaben wirst du genau das untersuchen und versuchen, selbst die Regel herauszufinden, mit der du einen (oder mehrere) Innenwinkel in jedem Dreieck bestimmen kannst, ohne jedes Mal nachmessen zu müssen.
Gleichseitige Dreiecke
Die Innenwinkel bleiben gleich. Egal wie du die Punkte A und B verschiebst, solange die Winkel gleich bleiben handelt sich weiterhin um ein gleichseitiges Dreieck.
Allgemeine Dreiecke
Innenwinkelsumme im Dreieck
Aufgaben
Bearbeite nun die untenstehenden Aufgaben. Beginne mit Aufgabe 5. Falls dir die Rechnungen leicht fallen, kannst du auch direkt zu Aufgabe 6 weitergehen. Wenn du Platz brauchst, um deine Rechnungen zu notieren, kannst du hierfür den Platz auf dem Arbeitsblatt nutzen.