Info
In diesem Lernpfadkapitel beschäftigst du dich mit Prismen.
Du lernst, das Prisma von anderen geometrischen Körpern abzugrenzen sowie die Oberfläche und das Volumen eines Prismas zu berechnen.
Dazu haben wir für dich Aufgaben in verschiedenen Schwierigkeitsstufen:
- Mit Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit
- und Aufgaben mit grünem Streifen sind Knobelaufgaben.
Wir wünschen dir viel Erfolg!
Das Prisma
Definition
Ein Prisma ist ein Körper, der durch zwei zueinander parallele und deckungsgleiche Vielecke sowie durch Rechtecke begrenzt wird.
Die beiden zueinander parallelen und deckungsgleichen Vielecke heißen Grundflächen und die Rechtecke Seitenflächen.
Alle Seitenflächen bilden zusammen die Mantelfläche des Prismas und als Höhe des Prismas wird der Abstand der Grundflächen voneinander bezeichnet.
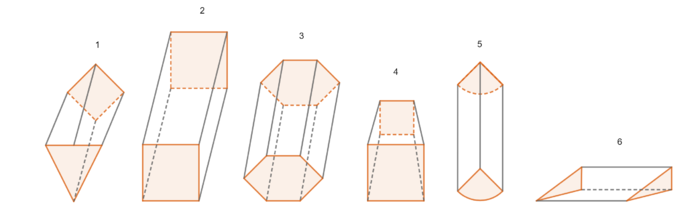
Vier Prismen mit unterschiedlichen, orange eingefärbten Grundflächen. Die Höhe der Prismen entspricht der Länge der schwarzen Linien.
Prismen und andere Körper
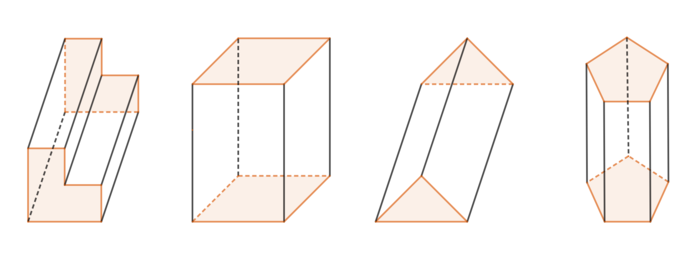
Aufgabe 1: Prismen erkennen
Welche der angegeben Körper sind Prismen?
Sechs geometrische Körper. Bei manchen handelt es sich um Prismen, bei anderen nicht.
(!1) (2) (3) (!4) (!5) (6)
- Körper 1 ist kein Prisma, da die Grundflächen verschiedene Vielecke sind, die somit nicht deckungsgleich sein können.
- Körper 2 ist ein Prisma mit quadratischen Grundflächen. Körper 2 ist zudem ein Quader.
- Körper 3 ist ein Prisma mit sechseckigen Grundflächen.
- Körper 4 ist kein Prisma, da die Grundflächen unterschiedlich groß und somit nicht deckungsgleich sind.
- Körper 5 ist kein Prisma, da die Grundflächen keine Vielecke, sondern Kreisschnitte sind.
- Körper 6 ist ein Prisma mit rechtwinkligen Dreiecken als Grundflächen.
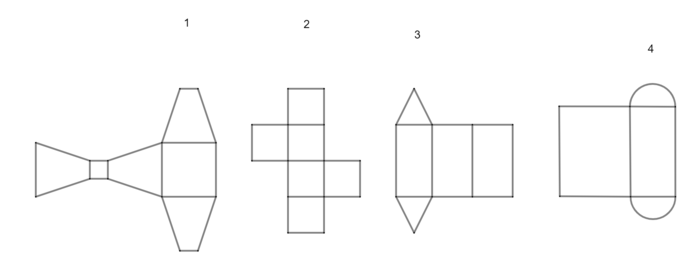
Aufgabe 2: Netze
Welches dieser Körpernetze kann man zu einem Prisma zusammensetzen? Solltest du nicht mehr wissen, was das Netz eines Körpers ist oder wie du es zeichnest, guck doch einmal hier nach.
- Netz 1 kann zu einer Pyramide mit abgeflachter Spitze, aber nicht zu einem Prisma zusammengesetzt werden.
- Netz 2 kann zu einem Würfel und damit zu einem Prisma zusammengesetzt werden
- Netz 3 kann zu einem Prisma mit dreieckigen Grundflächen zusammengesetzt werden.
- Netz 4 kann zu einem Zylinderschnitt, aber nicht zu einem Prisma zusammengesetzt werden.
Aufgabe 3: Körpernetz zeichnen
Zeichne das Netz eines Prismas mit folgenden Eigenschaften:
- Die Grundflächen sind Rechtecke, bei denen die langen Seiten doppelt so lang sind wie die kurzen.
- Das Prisma ist drei mal so hoch wie die langen Seite der Grundflächen lang sind.
- Zeichne zunächste eine der Grundflächen ein.
- Überlege, wie viele Seitenflächen das Prisma hat.
Dein gezeichnetes Netz könnte etwa so aussehen:
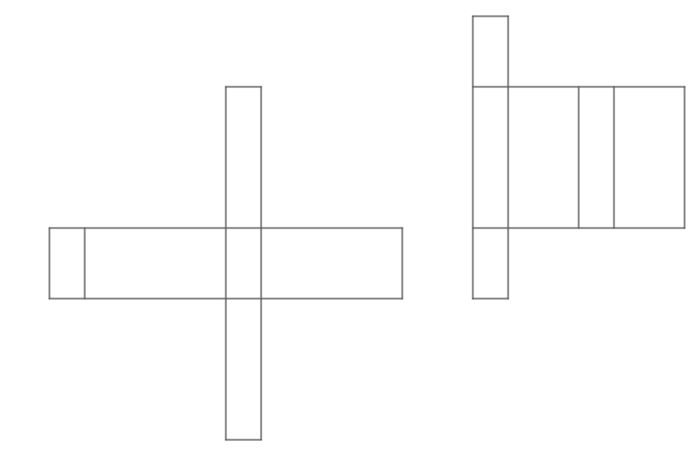
Beachte, dass es sehr viele Möglichkeiten gibt, ein Körpernetz zu zeichnen.
Veranschaulichung
Bewege den Regler "n", um die Grundflächen des Prismas zu verändern und den Regler "Öffnen", um zwischen Prisma und Körpernetz zu wechseln.
Aufgabe 4: Lückentext
Vielleicht sind dir bei den bisherigen Aufgaben schon Besonderheiten des Prismas und Unterschiede oder Gemeinsamkeiten zu anderen Körpern aufgefallen. Um dein Wissen zu vertiefen und das Erlernte zu festigen, fülle den folgenden Lückentext aus, indem du die korrekten Wörter in die jeweiligen Lücken ziehst.
Das Prisma besteht aus zwei Grundflächen, die deckungsgleich und parallel zueinander liegen. Der Abstand der Grundflächen zueinander wird als Höhe des Prismas bezeichnet. Miteinander verbunden werden die Grundflächen durch Rechtecke, die Seitenflächen genannt werden. Addierst du die Flächeninhalte aller Seitenflächen, erhältst du die Mantelfläche des Prismas. Im Vergleich mit anderen geometrischen Körpern fällt auf, dass alle Quader und Würfel Prismen sind, aber nicht jedes Prisma ein Quader oder Würfel ist. Und im Gegensatz zum Zylinder, der runde Grundflächen hat, sind die Grundflächen des Prismas eckig.
Vor dem Rechnen: Verständnis, Größen und Einheiten
1) Verständnis und Wiederholung
Wie macht man aus Strecken Flächen oder Volumen? Wann nutzt man Addition, wann Multiplikation? Warum haben einige Einheiten Exponenten (Hochzahlen)? Beantworte die folgenden Fragen, indem du auf das richtige Kästchen klickst!
Wie kann ich aus einer Strecke eine Fläche machen? (!Mit einer Strecke addieren) (Mit einer Strecke multiplizieren) (!Mit einer Fläche addieren) (!Mit einer Fläche multiplizieren)
Wie kann ich aus einer Strecke ein Volumen machen? (!Mit zwei weiteren Strecken addieren) (Mit zwei weiteren Strecken multiplizieren) (!Mit zwei weiteren Flächen addieren) (!Mit zwei weiteren Flächen multiplizieren)
Wie kann ich aus einer Fläche ein Volumen machen? (!Mit einer Strecke addieren) (Mit einer Strecke multiplizieren) (!Mit einer Fläche addieren) (!Mit einer Fläche multiplizieren)
Darf man Strecken, Flächen und Volumen miteinander addieren? (!Ja, ohne Einschränkungen) (!Nur wenn die Einheiten gleich sind, z.B. alle sind  ) (!Nur wenn die Einheiten gleich sind, bis auf den Exponent, z.B.
) (!Nur wenn die Einheiten gleich sind, bis auf den Exponent, z.B.  und
und  ) (Nur Strecken mit Strecken, Flächen mit Flächen, Volumen mit Volumen) (!Nein, niemals)
) (Nur Strecken mit Strecken, Flächen mit Flächen, Volumen mit Volumen) (!Nein, niemals)
Die Einheiten der Strecke stehen ohne Exponent, weil ... (!sie keinen brauchen) (!der Exponent 0 ist, und damit nicht geschrieben werden braucht) (der Exponent 1 ist, und damit nicht geschrieben werden braucht)
Die Exponenten bei den Einheiten ... (!dienen nur der besseren Unterscheidung) (!erhöhen sich mit der gleichen Anzahl an Additionen, maximal drei Additionen) (erhöhen sich mit der gleichen Anzahl an Multiplikationen, maximal drei Multiplikationen) (!sind willkürlich)
2) Ordnen
Strecken, Flächen und Volumen werden jeweils eigene Einheiten zugeordnet. Ordne die angegeben Einheiten richtig zu!
Oberfläche eines Prismas
In diesem Abschnitt beschäftigst du dich mit den unterschiedlichen Flächen des Prismas. Die vielen Seitenflächen, auch Mantelfläche genannt, ergeben gemeinsam mit den beiden Grundflächen die Oberfläche eines Prismas. Fügst du diese zu einem Körper zusammen, wird umgangssprachlich auch von einem Hohlkörper gesprochen.
1) Vermutung anstellen
Betrachte das Fünfeck und das Sechseck. Welche Regelmäßigkeiten vermutest du für beliebige n-Ecke im Hinblick auf die Flächenberechnung?
1. Man kann jedes regelmäßige n-Eck in n gleiche Dreiecke unterteilen.
2. Nach Bestimmung des Mittelpunkts und dessen Abstand zum Mittelpunkt einer Grundlinie kann man die Fläche jeden Dreiecks bestimmen.
Berechnung der Oberfläche eines regelmäßigen Prismas
Falls ihr einige der Grundlagen nicht mehr wißt, könnt ihr die Formeln hier nochmal nachschlagen.
Fläche

= Seite


Seite

Fläche

=

Aufgabe 2:
Fasse die folgenden Terme zusammen:
a) Dreiseitiges, rechtwinkliges Prisma:  cm,
cm,  cm und
cm und  cm; Körperhöhe
cm; Körperhöhe  cm
cm

Berechnung der Grundfläche:
 .
.
A: Der Flächeninhalt einer Grundfläche beträgt 
 .
.
Berechnung der Mantelfläche:
 .
.
A: Der Flächeninhalt der Mantelfläche beträgt 
 .
.
Berechnung der Oberfläche:
 .
.
A: Der Oberflächeninhalt beträgt


.
b)Prisma mit der Grundfläche eines Parallelogramm:  cm,
cm,  cm und
cm und  cm; Körperhöhe
cm; Körperhöhe  cm
cm

Aufgabe 3: Berechne die Fehlenden Größen
Bei einem Prisma sind G der Flächeninhalt einer Grundfläche, M der Mantelflächeninhalt und O der Oberflächenihalt:



Die Größen auf eine Maßeinheit bringen:

Einsetzten der Bekannten Größen in die bekannte Gleichung und anschließend wird nach M umgestellt:

Damit ist die fehlende Größe

Prismen mit unregelmäßiger Grundform
Es gibt auch Prismen mit unregelmäßiger Form der Grundflächen. Viele von diesen sind Kombinationen bekannter Flächen, z.B. unterschiedlichen Rechtecken und/oder Dreiecken. Sehr einfache Kombinationen sollen unten zusammengefasst werden.
Volumen eines Prismas
In diesem Abschnitt beschäftigst du dich mit dem Volumen eines Prismas. Aus einer Grundfläche und der Höhe ergibt sich der Inhalt eines Körpers. Du kannst dir hier einen Körper vorstellen, den man mit Wasser oder anderen Materialien füllt. Umgangssprachlich ein massiver Körper.
Berechnung des Volumens eines regelmäßigen Prismas
Die allgemeine Formel für das Volumen eines regelmäßigen Prismas lautet:
Volumen V = Grundfläche \cdot Höhe h
Herleitung Volumen Würfel
Text zum Verstecken
Herleitung Volumen Quader
Text zum Verstecken
Herleitung Volumen Prisma
Text zum Verstecken
Aufgabe 2:
Berechne das Volumen von Aufgabe 2:
a) Dreiseitiges, rechtwinkliges Prisma:  cm,
cm,  cm und
cm und  cm; Körperhöhe
cm; Körperhöhe  cm
cm

Berechnen des Volumens:

A: Das Volumen beträgt


.
b)Prisma mit der Grundfläche eines Parallelogramm:  cm,
cm,  cm und
cm und  cm; Körperhöhe
cm; Körperhöhe  cm
cm

Berechnen des Volumens:

A: Das Volumen beträgt


oder


.
Aufgabe 3: Berechne die Fehlenden Größen
Bei einem Prisma sind G der Flächeninhalt einer Grundfläche, M der Mantelflächeninhalt, O der Oberflächeninhalt, h die Höhe und V das Volumen des Körpers:




Die Größen auf eine Maßeinheit bringen:

Einsetzten der Bekannten Größen in die bekannte Gleichung und anschließend wird nach G umgestellt:

Einsetzten der Bekannten Größen in die bekannte Gleichung und anschließend wird nach h umgestellt:

A: Die Höhe h beträgt  und die Grundfläche ist
und die Grundfläche ist  .
.
Hinweis
Betrachte die drei Fotos! Die Karten sollen ein Prisma darstellen. Neben einem regelmäßigen Prisma, siehst du zwei schräge Prismen. Was verändert sich? Was bleibt gleich?