|
|
| Zeile 227: |
Zeile 227: |
| {{Lösung versteckt|Vergleiche deine Lösungen: | | {{Lösung versteckt|Vergleiche deine Lösungen: |
|
| |
|
| [[Datei:Von der allgemeinen Form in die Scheitelpunktform.jpg|rahmenlos|775x775px]]|Vergleiche deine Rechnungen|Verbergen}}
| | |Vergleiche deine Rechnungen|Verbergen}} |
|
| |
|
| {{Box|Übung 10 - online: allgemeine Form -> Scheitelpunktform|Löse so viele Aufgaben, bis zu mindestens 300 Punkte gesammelt hast. | | {{Box|Übung 10 - online: allgemeine Form -> Scheitelpunktform|Löse so viele Aufgaben, bis zu mindestens 300 Punkte gesammelt hast. |
SEITE IM AUFBAU
6 Die Normalform und die allgemeine Form quadratischer Funktionen
Eine Parabel, zwei Gleichungen...
Das nachfolgende GeoGebra-Applet zeichnet die Parabeln zu den Funktionsgleichungen. Erstelle eine Parabel in der Normalform und stelle anschließend d und e für die Scheitelpunktform so ein, dass die Graphen identisch sind.
Beschreibe deine Beobachtung.
Die Normalform quadratischer Gleichungen f(x) = x² + px + q und die allgemeine Form quadratischer Gleichungen f(x) = ax² + bx + c
Die quadratischen Funktionen der Form f(x) = x² + px + q haben die verschobene Normalparabel als Graphen.
Funktionen der Form f(x) = ax² + bx + c haben Parabeln als Graphen. Wandeln wir die Normalform bzw. die allgemeine Form in die Scheitelpunktform um, so lässt sich der Scheitelpunkt ablesen.
6.1 Von der Scheitelpunkform in die Normalform bzw. in die allgemeine Form
Eine Parabel, zwei Gleichungen
Stelle im Applet die Schieberegler so ein, dass die Graphen identisch sind. Z.B. d=-3; e=-4 und p=6; q=5. Begründe rechnerisch, dass die Gleichungen dieselbe Parabel beschreiben.

Scheitelpunktform:
f(x) = (x+3)² - 4 |Klammer auflösen: 1. binomische Formel
= x² + 6x + 9 - 4 |zusammenfassen
= x² + 6x + 5
Normalform: f(x) = x² + 6x + 5
Wiederholung: 1. und 2. binomische Formel
1. binomische Formel: (a + b)² = a² + 2ab + b² Beispiel: (x + 7)² = x² + 14x + 49
2. binomische Formel: (a - b)² = a² - 2ab + b² Beispiel: (x - 1,5)² = x² - 3x + 2,25
Kannst du noch die Quadratzahlen bis 25 auswendig? (Tipp unten)
Quadratzahlen:
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
18² = 324
19² = 361
20² = 400
25² = 625
Übung 1: Von der Scheitelpunktform zur Normalform - online
Löse so viele Aufgaben des nachfolgenden Applets, bis du dich beim Umwandeln sicher fühlst. Die Tipps helfen dir Schritt für Schritt zur Lösung.
Applet von Tinwing
Übung 2: Von der Scheitelpunktform zur Normalform - Aufgaben aus dem Buch
Löse die Aufgaben aus dem Buch. Prüfe deine Ergebnisse, indem du die Parablen mit dem Applet oben zeichnest. Sie müssen identisch sein.
- S. 17 Nr. 1
- S. 18 Nr. 7
- S. 18 Nr. 8
- S. 18 Nr. 10
Tipp: Löse mithilfe der 1. bzw. 2. binomischen Formel die Klammer auf und fasse zusammen zur Form f(x) = x² + px + q.
a) Tipp: (x+4)² = x² + 8x + 16,
also ist f(x) = (x+4)² + 7
= x² + 8x + 16 + 7
= x² + 8x + 23
b) Tipp: (x-5)² = x² - 10x + 25, also...
c) Tipp: (x-6)² = x² - 12x + 36
d) Tipp: (x+1)² = x² + 2x + 1
Löse mithilfe der 1. bzw. 2. binomischen Formel die Klammer auf und fasse zusammen zur Form f(x) = x² + px + q.
(x + 2,5)² = x² + 5x + 6,25
(x +  )² = x² + 3x +
)² = x² + 3x + 
(x + 1,5)² = x² + 3x + 2,25
Lies den Scheitelpunkt der Graphen im Schaubild ab, stelle die zugehörige Funktionsgleichung in der
Scheitelpunkform f(x) = (x + d)² + e auf. Forme anschließend die Scheitelpunkform in die Normalform um und ordne die passende Funktionsgleichung zu.
a) S(1|-2),
also ist f(x) = (x - 1)² - 2
umformen: f(x) = (x - 1)² - 2
= x² - 2x + 1 - 2
= x² - 2x - 1, also gehört (A) zu c).
Stelle im Applet oben die Scheitelpunktform passend zum gegebenen Scheitelpunkt ein und prüfe dein Ergebnis, indem du p und q in der Normalform einstellst. Wird dieselbe Parabel gezeichnet?
Stelle mithilfe des Scheitelpunktes S die zugehörige Funktionsgleichung in der Scheitelpunkform f(x) = (x + d)² + e auf. Forme anschließend die Scheitelpunkform in die Normalform um und ordne die passende Funktionsgleichung zu.
a) S(2|1),
also ist f(x) = (x - 2)² + 1
umformen: f(x) = (x - 2)² +1
= x² - 4x + 4 + 1
= x² - 4x +5
Übung 3: Von der Scheitelpunktform in die allgemeine Form
Forme die Funktionsgleichung der Funktion in der Scheitelpunktform in die allgemeine Form f(x) = ax² + bx + c um.
Beispiel:
f(x) = 2(x+2)² - 1 |1. binomische Formel anwenden
= 2(x² + 4x + 4) - 1 |ausmultiplizieren 
= 2x² + 8x + 8 - 1
= 2x² + 8x + 7
a) f(x) = 2(x-1)² + 0,5
b) f(x) = -0,2(x + 3)² + 4
c) f(x) = 0,5(x - 4)² - 6
Übung 4
Erstelle eine Aufgabe (mit ausführlicher Lösung) ähnlich zu Übungen 1, 2 bzw. 3 und lade sie im Mathematik-Ordner deiner Klasse hoch.
6.2 Von der Normalform in die Scheitelpunktform
Von der Normalform in die Scheitelpunktform
Stelle im Applet die Schieberegler erneut so ein, dass die Graphen identisch sind. Z.B. p=6; q=9 und d=-3;e=0. Erkennst du einen Zusammenhang?

Normalform:
f(x) = x² + 6x + 9 |Faktorisieren: 1. binomische Formel
= (x+3)²
Scheitelpunktform: f(x) = (x+3)²
Übung 5 - Faktorisieren mit binomischen Formeln (Wiederholung)
- Bearbeite Aufgaben des nachfolgenden Applets, bis du sicher beim Fakorisieren mit den binomischen Formeln bist.
- Löse die nachfolgenden LearningApps.
Applet von Reiner Hartl
Von der Normalform zur Scheitelpunktform
Gegeben ist die Funktionsgleichung einer quadratischen Funktion in der Normalform. Welches Problem stellt sich, wenn du hier mithilfe der 1. binomischen Formel faktorisieren möchtest?
f(x) = x² + 2x + 3
Diskutiere mit deinem Parter/deiner Parterin.
Habt ihr Lösungsvorschläge?
Das Problem ist nun, dass hier die Zahl "-3" nicht zur 1. binomischen Formel x² + 2x + ... "passt".
Welche Zahl "wünschst" du dir hier?
x² + 2x + 1, denn dies ist faktorisiert (x+1)²
Diese Methode heißt "quadratische Ergänzung". Erkläre!
Von der Normalform zur Scheitelpunktform
Lisa und Tim haben Ideen, wie sie die Normalform in die Scheitelpunktform umwandeln können. Erkläre und vergleiche.

 Lisa:
Lisa:
Normalform:
f(x) = x² + 2x + 3 |-3
f(x) - 3 = x² + 2x |quadratische Ergänzung: +1²
f(x) - 3 + 1² = x² + 2x + 1²
f(x) - 2 = (x + 1)² |+2
f(x) = (x+1)² + 2
Scheitelpunktform: f(x) = (x+1)² + 2,also lautet der Scheitelpunkt S(-1|2).
 Tim
Tim
Normalform:
f(x) = x² + 2x + 3 |quadratische Ergänzung: +1²
f(x) = x² + 2x + 1² - 1² + 3
f(x) = (x + 1)² -1 + 3
f(x) = (x+1)² + 2
Scheitelpunktform: f(x) = (x+1)² + 2, also lautet der Scheitelpunkt S(-1|2).
Von der Normalform zur Scheitelpunktform - Quadratische Ergänzung
Die Funktionsgleichung f(x)=x² + px + q in der Normalform lässt sich durch quadratische Ergänzung
in die Scheitelpunktform f(x)=(x + d)² + e umwandeln, um die Koordinaten des Scheitelpunktes S(-d|e) abzulesen.
Übung 1-Vorübungen quadratische Ergänzung
Löse die nachfolgenden LearningApps.
Übung 6 - online: Normalform -> Scheitelpunktform
Löse so viele Aufgaben, bis zu mindestens 300 Punkte gesammelt hast.
Übung 7 - Von der Normalform in die Scheitelpunktform
Löse die Aufgaben aus dem Buch. Prüfe deine Ergebnisse, indem du die Parabeln mit dem Applet oben zeichnest. Sie müssen identisch sein.
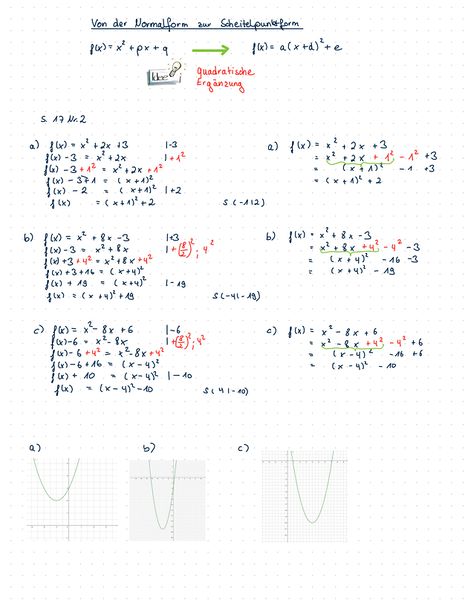
- S. 17 Nr. 2
- S. 18 Nr. 3
- S. 18 Nr. 4
- S. 18 Nr. 5
- S. 18 Nr. 11
Ausführliche Lösungen:

Übung 8: Aufgaben erfinden
1. Einzelarbeit
- Zeichne eine beliebige Normalparabel in ein Koordinatensystem.
- Bestimme den Scheitelpunkt.
- Bestimme die Scheitelpunktform.
- Forme in die Normalform um.
2. Partnerarbeit
- Nenne deinem Partner/deiner Partnerin deine Gleichung in der Normalform.
- Wandle nun diese Normalform in die Scheitelpunktform um und gib den Scheitelpunkt an.
Erhältst du die Ausgangsgleichung?
6.3 Von der allgemeinen Form quadratischer Funktionen in die Scheitelpunktform
Sind Funktionsgleichungen quadratischer Funktionen in der allgemeinen Form f(x) = ax² + bx + c gegeben, kann auch hier mithilfe der quadratischen Ergänzung in die Scheitelpunkform f(x) = a (x + d)² + e umgeformt und der Scheitelpunkt S(-d|e)abgelesen werden.
 Tipp: Klammere den Faktor a zunächst aus und gehe dann wie geübt vor.
Tipp: Klammere den Faktor a zunächst aus und gehe dann wie geübt vor.
Von der allgemeinen Form in die Scheitelpunktform
Forme die Funktionsgleichung
f(x) = -0,25x² + 2x + 1
von der allgemeinen Form in die Scheitelpunktform um und lies den Scheitelpunkt S ab.
Prüfe deine Lösung mithilfe von GeoGebra.
Klammere den Faktor a = -0,25 aus.
f(x) = -0,25x² + 2x + 1 |Teile jeden Summanden durch -0,25
=0,25 (x² - 8x - 4) | Forme nun mithilfe der quadratischen Ergänzung den Term in der Klammer zu einer binomischen Formel um.
Klammere den Faktor a = -0,25 aus.
f(x) = -0,25x² + 2x + 1 |Teile jeden Summanden durch -0,25
=0,25 (x² - 8x - 4) | q E 
= -0,25 (x² - 8x +
4² - 4² - 4) |Faktorisiere und multipliziere aus.
Klammere den Faktor a = -0,25 aus.
f(x) = -0,25x² + 2x + 1 |Teile jeden Summanden durch -0,25
=-0,25 (x² - 8x - 4) | q E 
= -0,25 (x² - 8x + 4² - 4² - 4) |Faktorisiere
= -0,25 ((x - 4)² - 16 - 4) |fasse zusammen
= -0,25 ((x - 4)² - 20) |ausmultiplizieren
= -0,25 (x - 4)² + 5
Scheitelpunkt S(4|5)
Übung 9: Von der allgemeinen Form in die Scheitelpunktform
Wandle die Funktionsgleichungen von der allgemeinen Form in die Scheitelpunktform um und lies den Scheitelpunkt ab. Handelt es sich um einen Hoch- oder Tiefpunkt?
a) f(x) = 2x² + 4x + 2
b) f(x)= -0,3x² + 0,9x + 1,2
c) f(x) = 0,5x² + 7x
Prüfe deine Lösung mit GeoGebra.
Vergleiche deine Lösungen:
Übung 10 - online: allgemeine Form -> Scheitelpunktform
Löse so viele Aufgaben, bis zu mindestens 300 Punkte gesammelt hast.
IDEENSAMMLUNG
Modellieren
Aufgabe Basektball (mit Lösungsschritten)







 Tipp: Klammere den Faktor a zunächst aus und gehe dann wie geübt vor.
Tipp: Klammere den Faktor a zunächst aus und gehe dann wie geübt vor.









