Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Multiplizieren: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (46 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}}<br> | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
<br> | |||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Navigation|[[Herta-Lebenstein-Realschule/Rechnen mit Brüchen| 0) Vorwissen]]<br> | {{Navigation|[[Herta-Lebenstein-Realschule/Rechnen mit Brüchen| 0) Vorwissen]]<br> | ||
[[Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Addieren und Subtrahieren|1) Addieren und subtrahieren von Brüchen]]<br> | [[Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Addieren und Subtrahieren|1) Addieren und subtrahieren von Brüchen]]<br> | ||
| Zeile 10: | Zeile 12: | ||
===2.1 Brüche mit einer natürlichen Zahl multiplizieren (Vervielfachen)=== | ===2.1 Brüche mit einer natürlichen Zahl multiplizieren (Vervielfachen)=== | ||
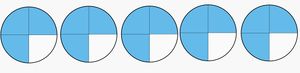
{{Box|Vervielfachen von Brüchen|Nutze das nachfolgende GeoGebra-Applet. Stelle zunächst | {{Box|Vervielfachen von Brüchen|Lege und löse:<br> | ||
[[Datei:Fünf mal drei Viertel Brüche .jpg|rahmenlos]] | |||
Notiere Aufgaben zu diesem Bild und löse sie.|Unterrichtsidee}} | |||
{{Box|Vervielfachen von Brüchen - Übung 1|Nutze das nachfolgende GeoGebra-Applet. Stelle zunächst die Schieberegler für Multiplikator, Nenner und passend zur Aufgabe ein. Notiere mindestens 3 Aufgaben in dein Heft.<br> | |||
Fällt dir etwas auf?<br> | |||
Kannst du eine Regel formulieren?|Üben}} | |||
{{Lösung versteckt|Möglicher Satzanfang für eine Regel:<br> | |||
Ich multipliziere einen Bruch mit einer natürlichen Zahl, indem ich ...|Tipp 1 zur Regel|Schließen}} | |||
{{Lösung versteckt|Verwende z.B. die Wörter "Zähler", "Nenner", "natürliche Zahl", "multipizieren"|Tipp 2 (Wörterlisten)|Schließen}} | |||
Direkter Link, falls das Applet nicht passend dargestellt wird: https://www.geogebra.org/m/cK6jYx5B | Direkter Link, falls das Applet nicht passend dargestellt wird: https://www.geogebra.org/m/cK6jYx5B | ||
| Zeile 18: | Zeile 27: | ||
<small>Applet GeoGebra Translation Team German</small> | <small>Applet GeoGebra Translation Team German</small> | ||
{{Box|Hefteintrag: Multiplikation eines Bruches mit einer Zahl (Vervielfachen)| | |||
[[Datei:Merkkasten - Vervielfachen von Brüchen.jpg|800x800px]]|Arbeitsmethode}} | |||
{{#ev:youtube|RohwoJ3XpeI|800|center}} | |||
{{LearningApp|app=p45e9kcun20|width=100%|height=600px}} | |||
{{Box|Übung 2 (online)|Löse auf der Seite realmath so viele Aufgaben, dass du jeweils mindestens 300 Punkte erreichst. | |||
* [https://realmath.de/Neues/Klasse6/kuerzen/zahlmalbruch01.php Zahl mal Bruch 1] | |||
* [https://realmath.de/Neues/Klasse6/kuerzen/zahlmalbruch02.php Zahl mal Bruch 2 (hier musst du das Ergebnis kürzen!)]|Üben}} | |||
{{Box|Übung 3 Buch|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und berechne ausführlich. Falls möglich, kürze zuerst! | |||
* S. 63 Nr. 4 | |||
* S. 63 Nr. 5 | |||
* S. 63 Nr. 6 | |||
* S. 63 Nr. 7 (Knobelaufgabe)|Üben}} | |||
{{Lösung versteckt|Nutze das obige GeoGebra-Applet, wenn du unsicher bist.|Tipp zu Übung 3|Schließen}} | |||
{{Box|Übung 4 - Anwendungsaufgabe|Leonie möchte zu ihrem Geburtstag für ihre Familie einen Kuchen backen. Für den Teig benötigt sie <math>\frac{1}{6}</math> Butter, <math>\frac{1}{8}</math> Marzipan-Rohmasse, <math>\frac{1}{10}</math> braunen Zucker, 2 Prisen Salz, 4 Eier, <math>\frac{1}{10}</math> kg Weizenmehl, 1 Packung Backpulver und <math>\frac{1}{6}</math> Schokoblättchen.<br> | |||
Da ihre Familie sehr groß ist, nimmt sie die dreifache Masse. Welche Mengen benötigt sie für die Schokoblättchen und den braunen Zucker?|Üben}} | |||
<br> | |||
{{Lösung versteckt|1=<br> | |||
Für die Butter und die Schokoblättchen muss Sie folgendes rechnen: <br> | |||
<math>\frac{1}{6}</math> + <math>\frac{1}{6}</math> + <math>\frac{1}{6}</math> = <math>\frac{1+1+1}{6}</math>= <math>\frac{3}{6}</math> = <math>\frac{1}{2}</math> | |||
Für den braunen Zucker und das Weizenmehl lautet die Rechnung: | |||
<math>\frac{1}{10}</math> + <math>\frac{1}{10}</math> + <math>\frac{1}{10}</math> = <math>\frac{1+1+1}{10}</math>= <math>\frac{3}{10}</math> | |||
|2=Lösung|3=Schließen}} | |||
===2.2 Brüche multiplizieren (Bruch mal Bruch)=== | ===2.2 Brüche multiplizieren (Bruch mal Bruch)=== | ||
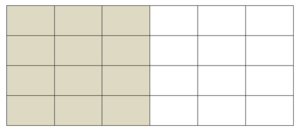
{{Box|Brüche multiplizieren - Einstieg|Von einer Schokolade ist die Hälfte übrig.<br> | |||
Julia sagt: „ Davon schaff ich <math>\tfrac{3}{4}</math> “. <br> | |||
[[Datei:Schokolade Einführung Mulitplikation von Brüchen.png|rahmenlos]]<br> | |||
Welchen Anteil schafft Julia von der ganzen Tafel Schokolade?|Frage}} | |||
{{Lösung versteckt|Die Hälfte der Schokolade ist markiert, von dieser Hälfte müssen wir jetzt <math>\tfrac{3}{4}</math> bestimmen.|Tipp 1|Schließen}} | |||
{{Lösung versteckt|<math>\tfrac{1}{2}</math>∙<math>\tfrac{3}{4}</math> bedeutet <math>\tfrac{1}{2}</math> von <math>\tfrac{3}{4}</math>|Tipp 2|Schließen}} | |||
{{Box|Erarbeitung: Brüche multiplizieren|Stelle im nachfolgenden GeoGebra-Applet die Multiplikation zweier Brüche dar. | |||
* Notiere die zugehörige Aufgabe und die Lösung in dein Heft. | |||
* Fällt dir etwas auf? | |||
* Kannst du eine Regel formulieren?|Frage}} | |||
https://www.geogebra.org/m/rtfv8qwt | |||
<ggb_applet id="fdxczgbs" width="800" height="560" border="888888" /> | |||
<small>Applet von Serlo Education</small> | |||
{{Box|Hefteintrag: Brüche multiplizieren (Bruch mal Bruch)|[[Datei:Merkkasten - Brüche multiplizieren neu.jpg|800x800px]]|Arbeitsmethode}} | |||
{{#ev:youtube|dYL1cta-Xnc|800|center}} | |||
{{LearningApp|app=pvx4jv12v20|width=100%|height=600px}} | |||
{{Box|Übung 3 (online)|Löse auf der Seite realmath so viele Aufgaben, dass du jeweils mindestens 300 Punkte erreichst. | |||
* [https://realmath.de/Neues/Klasse6/kuerzen/multiplizieren00.php Level 1] | |||
* [https://realmath.de/Neues/Klasse6/kuerzen/multiplizieren01.php Level 2] | |||
* [https://realmath.de/Neues/Klasse6/kuerzen/multiplizieren02.php Level 3] | |||
* [https://realmath.de/Neues/Klasse6/bruchdiv/multcool.php Vorsicht: nur für Profis] | |||
* [https://realmath.de/Neues/Klasse6/bruchmult/pyramidemulbruch3a.php Pyramide] | |||
* [https://realmath.de/Neues/Klasse6/bruchmult/pyramidemulbruch5.php Pyramide für Profis] | |||
* [https://realmath.de/Neues/Klasse6/kuerzen/dreimult01.php Drei Brüche multiplizieren]|Üben}} | |||
{{Box|1=Übung 4 (Heft)|2=Löse die nachfolgenden Aufgaben im Heft. Schreibe die Aufgabe ab und berechne ausführlich. Falls möglich, kürze zuerst!<br> | |||
a) <math>\tfrac{1}{4}\cdot\tfrac{2}{5}</math><br> | |||
<math>\tfrac{5}{8}\cdot\tfrac{4}{5}</math><br> | |||
<math>\tfrac{7}{9}\cdot\tfrac{3}{10}</math><br> | |||
b) <math>\tfrac{6}{11}\cdot\tfrac{5}{8}</math><br> | |||
<math>\tfrac{10}{3}\cdot\tfrac{3}{5}</math><br> | |||
<math>\tfrac{2}{9}\cdot\tfrac{5}{12}</math><br> | |||
c) <math>\tfrac{15}{16}\cdot\tfrac{12}{35}</math><br> | |||
<math>\tfrac{7}{30}\cdot\tfrac{20}{21}</math><br> | |||
<math>\tfrac{21}{48}\cdot\tfrac{16}{35}</math><br> | |||
d) <math>\tfrac{9}{14}\cdot\tfrac{7}{15}</math><br> | |||
<math>\tfrac{18}{35}\cdot\tfrac{7}{15}</math><br> | |||
<math>\tfrac{27}{55}\cdot\tfrac{5}{9}</math> | |||
|3=Üben}} | |||
{{Lösung versteckt|[[Datei:Multiplikation von Brüchen Übung 4 neu.jpg|rahmenlos|764x764px]]|Vergleiche deine Lösungen|Verbergen}} | |||
{{Box|Übung 5 (7er Buch)|Löse die Aufgaben aus dem 7er Buch. Schreibe die Aufgabe ab und löse ausführlich. Kürze falls möglich vor dem Multiplizieren und wandle das Ergebnis in die gemischte Schreibweise um (falls möglich). | |||
* S. 11 Nr. 1 | |||
* S. 11 Nr. 2 | |||
* S. 11 Nr. 5|Üben}} | |||
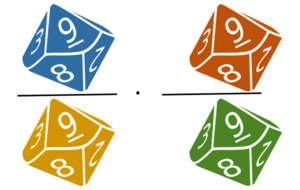
{{Box|Übung 6 Würfelspiel mit dem Partner/der Partnerin|Würfle mit vier 10er-Würfeln. Bildet aus den Augenzahlen zwei Brüche und multipliziert diese. | |||
[[Datei:Brüche multiplizieren Würfelspiel.PNG|rahmenlos|300x300px]]<br> | |||
<small>Vorsicht: Der Nenner darf NIE 0 sein, denn durch 0 dürfen wir nicht teilen.</small><br> | |||
Stellt Bedingungen auf, mit denen ihr den Sieger/die Siegerin ermittelt, z.B. größtes Produkt o.ä.|Üben}} | |||
{{Box|Übung 7 - Anwendungsaufgabe (7er Buch)|Löse die Aufgabe aus dem 7er Buch. Schreibe zuerst auf, was gegeben und was gesucht ist.<br> | |||
* S. 12 Nr. 15|Üben}} | |||
===2.3 Brüche in gemischter Schreibweise multiplizieren=== | ===2.3 Brüche in gemischter Schreibweise multiplizieren=== | ||
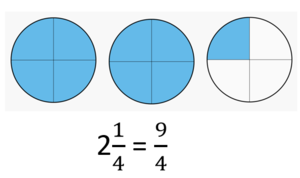
{{Box|Erinnerung: gemischte Schreibweise - unechter Bruch|So wandelst du die gemischte Schreibweise in einen unechten Bruch um: | |||
[https://www.alice.edu.tum.de/bruchrechnen.html#/ Schaue hier auf S. 52].<br> | |||
[[Datei:Zwei ein viertel gleich neun viertel.png|rahmenlos]]|Hervorhebung1}} | |||
{{#ev:youtube|FYAB-IVdJxc|800|center}} | |||
{{LearningApp|app=pkkm27e4n20|width=100%|height=600px}} | |||
{{Box|1= Übung 8 - Brüche in gemischter Schreibweise multiplizieren|2=Wandle die Brüche in unechte Brüche um und multipliziere.<br> | |||
a) 1<math>\tfrac{2}{3}</math>·2<math>\tfrac{2}{3}</math><br> | |||
b) 2<math>\tfrac{1}{4}</math>·<math>\tfrac{3}{5}</math><br> | |||
c) 3<math>\tfrac{1}{2}</math>·1<math>\tfrac{2}{5}</math><br> | |||
d) 4<math>\tfrac{4}{7}</math>·2<math>\tfrac{3}{8}</math>|3=Üben}} | |||
{{Box|Übung 9 - ANTON|Nun bist du fit und kannst die Aufgaben zur Multiplikation bei [https://anton.app/de/ '''ANTON'''] lösen.|Üben}} | |||
{{Box|1=Übung 10 - freiwillige Übung|2=Bearbeite auf den nachfolgenden Seiten weitere Aufgaben. | |||
* [https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Bruchrechnung Matheaufgabennet] Wähle dazu die Rechenart Muliplikation aus.|3=Üben}} | |||
{{Fortsetzung|weiter=3) Dividieren von Brüchen|weiterlink=Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Dividieren}} | {{Fortsetzung|weiter=3) Dividieren von Brüchen|weiterlink=Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Dividieren}} | ||
Aktuelle Version vom 16. November 2024, 07:30 Uhr
0) Vorwissen
1) Addieren und subtrahieren von Brüchen
2) Multiplizieren von Brüchen
3) Dividieren von Brüchen
4) Verbindung der Rechenarten
2 Brüche multiplizieren
2.1 Brüche mit einer natürlichen Zahl multiplizieren (Vervielfachen)
Möglicher Satzanfang für eine Regel:
Verwende z.B. die Wörter "Zähler", "Nenner", "natürliche Zahl", "multipizieren"
Direkter Link, falls das Applet nicht passend dargestellt wird: https://www.geogebra.org/m/cK6jYx5B

Applet GeoGebra Translation Team German
Nutze das obige GeoGebra-Applet, wenn du unsicher bist.
Für die Butter und die Schokoblättchen muss Sie folgendes rechnen:
+ + = = =
Für den braunen Zucker und das Weizenmehl lautet die Rechnung:
2.2 Brüche multiplizieren (Bruch mal Bruch)
Die Hälfte der Schokolade ist markiert, von dieser Hälfte müssen wir jetzt bestimmen.
∙ bedeutet von
https://www.geogebra.org/m/rtfv8qwt

Applet von Serlo Education
2.3 Brüche in gemischter Schreibweise multiplizieren