Herta-Lebenstein-Realschule/Lernpfad Prozentrechnung/1) Absoluter und relativer Vergleich: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 125: | Zeile 125: | ||
Wir können Anteile als Brüche, als Dezimalbrüche und in Prozent vergleichen. | Wir können Anteile als Brüche, als Dezimalbrüche und in Prozent vergleichen. | ||
{{Box|Relativer Vergleich|Um die Anteile vergleichen zu können, müssen wir also die Brüche gleichnamig machen oder sie in einen Dezimalbruch oder in Prozent umwandeln.|Arbeitsmethode}} | {{Box|Relativer Vergleich|Um die Anteile vergleichen zu können, müssen wir also die Brüche gleichnamig machen oder sie in einen Dezimalbruch oder in Prozent umwandeln.|Arbeitsmethode}} | ||
{{Lösung versteckt|1=Umwandlung: Bruch - Dezimalbruch | {{Lösung versteckt|1=Umwandlung: Bruch - Dezimalbruch<br> | ||
1) Ein Bruch kann durch Erweitern und Kürzen auf zehntel, hundertstel,… in einen Dezimalbruch umgewandelt werden | 1) Ein Bruch kann durch Erweitern und Kürzen auf zehntel, hundertstel,… in einen Dezimalbruch umgewandelt werden | ||
| Zeile 207: | Zeile 207: | ||
* S. 133 Nr. 10|Üben}} | * S. 133 Nr. 10|Üben}} | ||
{{Lösung versteckt|1= Tipp zu Nr. 6|2=Verbergen}} | {{Lösung versteckt|1= geg: Würfe insgesamt und jeweilige Treffer<br> | ||
ges: relative Häufigkeit<br> | |||
Jens: 7 Treffer von 15 Würfen, also <math>\frac{\text{Anzahl der Treffer}}{\text{Anzahl der Würfe insgesamt}}</math> = <math>\tfrac{7}{15}</math><br> | |||
Manuel: 9 Treffer von 20 Würfen insgesamt, also <math>\tfrac{9}{20}</math><br> | |||
Brüche vergleichen: | |||
* gleichnamig machen (Hauptnenner 60) | |||
* umwandeln in eine Dezimalzahl (Division)|2=Tipp 1 zu Nr. 6|3=Verbergen}} | |||
{{Lösung versteckt|1="Gleichnamig machen" - Wie geht das noch mal?<br> | |||
Erweitere beide Brüche auf denselben Nenner.<br> | |||
<math>\tfrac{7}{15}</math> = <math>\tfrac{7·4}{15·4}</math> = <math>\tfrac{28}{60}</math><br> | |||
<math>\tfrac{9}{20}</math> = <math>\tfrac{9·3}{20·3}</math> = <math>\tfrac{17}{60}</math><br> | |||
Welcher Bruch ist nun der größere?|2=Tipp 2 zu Nr. 6|3=Verbergen}} | |||
{{Lösung versteckt|1="Umwandeln in einen Dezimalbruch mit Division" - Wie geht das noch mal?<br> | |||
Schreibe statt des Bruchstrichs ein Geteilt-Zeichen. | |||
<math>\tfrac{7}{15}</math> = 7 : 15.<br>[[Datei:7 15tel als Dezimalbruch.jpg|rahmenlos]]<br> | |||
<math>\tfrac{9}{20}</math> kannst du ebenso in einen Dezimalbruch umwandeln.<br> | |||
Hier hast du zusätzlich die (schnellere) Möglichkeit, den Bruch so zu erweitern, dass der Nenner 100 beträgt und du den Dezimalbruch daran ablesen kannst.<br> | |||
|2=Tipp 3 zu Nr. 6|3=Verbergen}} | |||
{{Lösung versteckt|1=Du kannst die Klassen vergleichen, indem du das gesammelte Gewicht pro Schüler berechnest (relative Häufigkeit).<br> | |||
<math>\frac{\text{gesammeltes Gewicht}}{\text{Anzahl der Schüler}}</math> |2=Tipp zu Nr. 7|3=Verbergen}} | |||
{{Lösung versteckt|1=Vergleiche den erzielten Gewinn bezogen auf die Höhe des Einsatzes.<br> | |||
relative Häufigkeit=<math>\frac{\text{erzielter Gewinn}}{\text{Einsatz}}</math>|2=Tipp zu Nr. 9b|3=Verbergen}} | |||
{{Box|Übung 3 - online|Bearbeite die nachfolgenden GeoGebra-Applets des FLINK- Teams. Wähle den Originallink, falls nötig.| Üben}} | |||
Originallink https://www.geogebra.org/m/pprrjujw | |||
<ggb_applet id="y4f4xtjj" width="636" height="585" border="888888" /> | |||
Originallink https://www.geogebra.org/m/vvnawdmw | |||
<ggb_applet id="czgahwdj" width="726" height="549" border="888888" /> | |||
Originallink https://www.geogebra.org/m/w7ztgqmp | |||
<ggb_applet id="kvwuntqg" width="738" height="622" border="888888" /> | |||
Originallink https://www.geogebra.org/m/pswqud2f | |||
<ggb_applet id="q4kfnwzr" width="734" height="598" border="888888" /> | |||
Originallink https://www.geogebra.org/m/fefvmjbw<br> | |||
<ggb_applet id="ndru9r7t" width="609" height="640" border="888888" /> | |||
Originallink https://www.geogebra.org/m/ke7xbcwj | |||
<ggb_applet id="nqhwqbaf" width="750" height="550" border="888888" /> | |||
<small>Applets FLINK-Team</small> | |||
{{Fortsetzung|weiter=2) Prozentschreibweise|weiterlink=Herta-Lebenstein-Realschule/Lernpfad Prozentrechnung/2) Prozentschreibweise|vorher=zurück zur Startseite|vorherlink=Herta-Lebenstein-Realschule/Lernpfad Prozentrechnung}} | {{Fortsetzung|weiter=2) Prozentschreibweise|weiterlink=Herta-Lebenstein-Realschule/Lernpfad Prozentrechnung/2) Prozentschreibweise|vorher=zurück zur Startseite|vorherlink=Herta-Lebenstein-Realschule/Lernpfad Prozentrechnung}} | ||
Aktuelle Version vom 23. März 2024, 20:19 Uhr
1) Absoluter und relativer Vergleich
Führe das folgende Experiment durch: Stelle einen leeren Mülleimer in 3 m Entfernung von deinem Standort auf und versuche, einen kleinen Ball in den Eimer zu werfen. Alle Jungen haben 20 Versuche, alle Mädchen 25 Versuche.
Schicke dein Ergebnis an deine Mathelehrerin. Sie sammelt die Ergebnisse der Klasse...
...Hier sind die gesammelten Ergebnisse eurer Klasse:
| Name | Mats | Lisa | Kassem | Ida | Larissa | Henry | |
|---|---|---|---|---|---|---|---|
| Würfe insgesamt | 20 | 25 | 20 | 25 | 25 | 20 | |
| Eintrag folgt | Treffer | 10 | 11 | 13 | 12 | 17 | 12 |
| Eintrag folgt | hier folgen Einträge |
Wer war die beste Werferin/ der beste Werfer? Wer steht auf Platz zwei und drei?
Begründe deine Wahl!
Wir können die Zahlen auf zwei Arten miteinander vergleichen:
Wir ergänzen die Tabelle:
| Name | Mats | Lisa | Kassem | Ida | Larissa | Henry | |
|---|---|---|---|---|---|---|---|
| Würfe insgesamt | 20 | 25 | 20 | 25 | 25 | 20 | |
| Absoluter Vergleich | Treffer | 10 | 11 | 13 | 12 | 16 | 12 |
| Relativer Vergleich |
|
① Absolut gesehen hat LARISSA die meisten Treffer.
② Für den relativen Vergleich müssen wir die Anteile betrachten.
Wir können Anteile als Brüche, als Dezimalbrüche und in Prozent vergleichen.
Umwandlung: Bruch - Dezimalbruch
1) Ein Bruch kann durch Erweitern und Kürzen auf zehntel, hundertstel,… in einen Dezimalbruch umgewandelt werden
= = 0,6
2) Durch eine Divisionsaufgabe:
= 7 : 15 = 0,46 ≈ 0,467| Name | Bruch | Dezimalbruch | Prozent |
|---|---|---|---|
| Mats | = | 0,5 | 50% |
| Lisa | = | 0,44 | 44% |
| Kassem | = | 0,65 | 65% |
| Ida | = | 0,48 | 48% |
| Larissa | = | 0,64 | 64% |
| Henry | = | 0,6 | 60% |
Auswertung des Experiments: Mathematisch begründete Antwort auf die Einstiegsfrage
Kassem hat also gewonnen, denn 65 % seiner Würfe haben den Eimer getroffen.
Larissa hatte zwar absolut gesehen mehr Treffer aber „nur“ 64% ihrer Würfe haben den Eimer getroffen.
geg:7c 24 von 32 Sportabzeichen; 7b 20 von 25 Sportabzeichen
ges: relativer Vergleich7c ===75%
7b ==80%
geg: Würfe insgesamt und jeweilige Treffer
ges: relative Häufigkeit
Jens: 7 Treffer von 15 Würfen, also =
Manuel: 9 Treffer von 20 Würfen insgesamt, also
Brüche vergleichen:
- gleichnamig machen (Hauptnenner 60)
- umwandeln in eine Dezimalzahl (Division)
"Gleichnamig machen" - Wie geht das noch mal?
Erweitere beide Brüche auf denselben Nenner.
= =
= =
"Umwandeln in einen Dezimalbruch mit Division" - Wie geht das noch mal?
Schreibe statt des Bruchstrichs ein Geteilt-Zeichen.
= 7 : 15.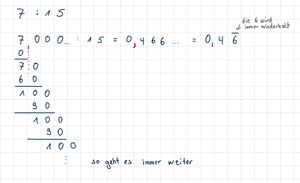
kannst du ebenso in einen Dezimalbruch umwandeln.
Du kannst die Klassen vergleichen, indem du das gesammelte Gewicht pro Schüler berechnest (relative Häufigkeit).
Vergleiche den erzielten Gewinn bezogen auf die Höhe des Einsatzes.
Originallink https://www.geogebra.org/m/pprrjujw

Originallink https://www.geogebra.org/m/vvnawdmw

Originallink https://www.geogebra.org/m/w7ztgqmp

Originallink https://www.geogebra.org/m/pswqud2f

Originallink https://www.geogebra.org/m/fefvmjbw

Originallink https://www.geogebra.org/m/ke7xbcwj

Applets FLINK-Team



