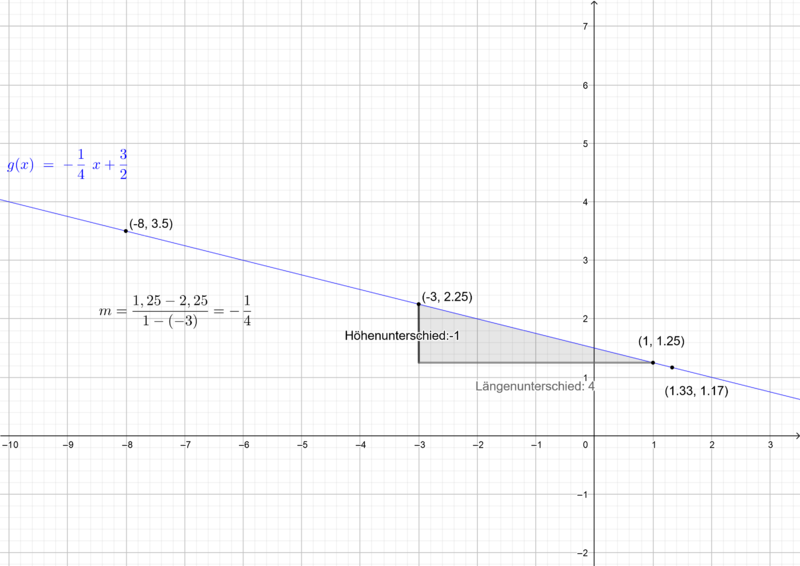
Maria möchte im Internet surfen und begutachtet die Tarife A, B und C.
Betrachte zunächst die Einheiten und versuche diese umzuformen.
Wie könntest du die Wert in €/h umgewandelt werden?
Wenn du diesen Wert hast, kannst du eine vorübergehende Funktionsgleichung mit  dem Wert €/h
dem Wert €/h  (einen noch unbekannten Wert) aufstellen.
(einen noch unbekannten Wert) aufstellen.
Wenn du

Stunden frei hast heißt dies, dass du in den

Stunden nur die Grundgebühr bezahlen musst.
Welchen Punkt erhalten wir dadurch?
Versuche dies in die Funktionsgleichung mit einzubauen indem du den Punkt einsetzt und die Gleichung auflöst.
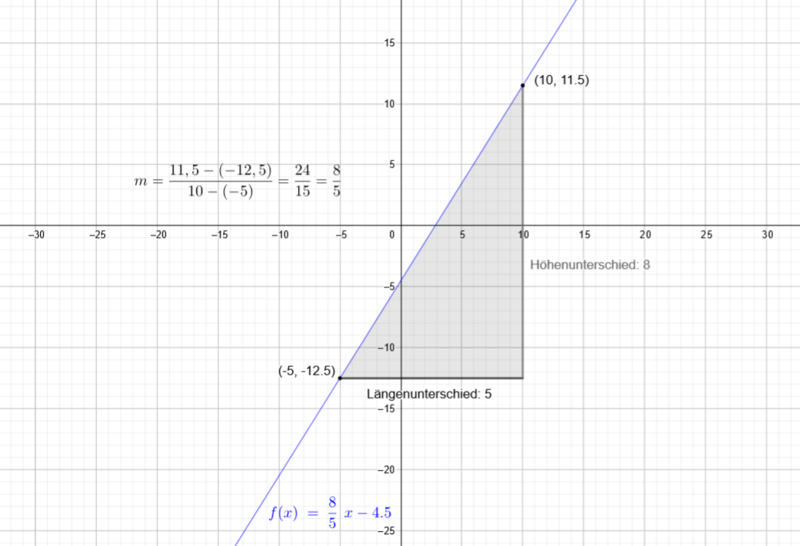
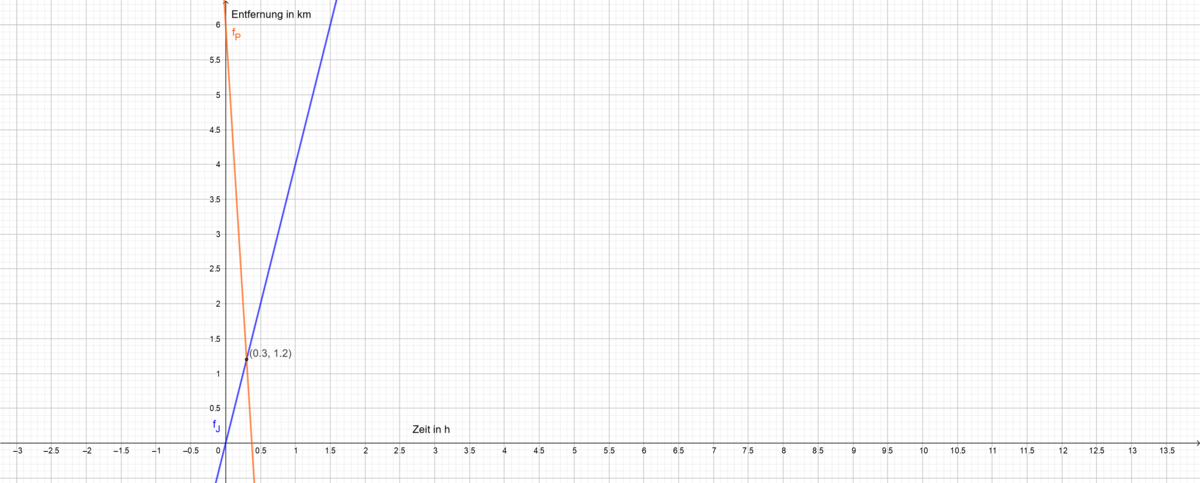
Um die Funktionsgleichung in ein Koordinatensystem zu übertragen, überlege dir zunächst welche Werte deine  - Achse und, welche Werte deine
- Achse und, welche Werte deine  -Achse angibst.
-Achse angibst.
Probiere einen geeigneten Maßstab zu wählen indem du vorher einige Werte (auch höhere) in die Funktionsgleichung eingibst.
Falls du mit dem Zeichnen von Graphen Schwierigkeiten hast, wiederhole das entsprechende Kapitel in diesem Lernpfad. Da werden dir zwei Möglichkeiten einen Graphen zu zeichnen vorgestellt.
Bedenke bei den Graphen von f und h jedoch, dass diese in einem bestimmten Bereich konstant sind.
Um den günstigen Tarif für Maria zu berechnen, müssen wir zunächst aus der Aufgabe herauslesen wie lange Maria im Monat surft.
Sie surft  h am Tag. Diesen Wert muss man jetzt noch auf den Monat umrechnen. Wie viele Stunden surft Maria in 30 Tagen (einem Monat)?
h am Tag. Diesen Wert muss man jetzt noch auf den Monat umrechnen. Wie viele Stunden surft Maria in 30 Tagen (einem Monat)?
Nun kannst du den Stunden Wert in die verschiedenen Funktionsgleichungen für

einsetzten, da die

- Achse die Stundenzahl angibt. Wenn du alle Werte der verschiedenen Funktionsgleichungen hast vergleiche diese.
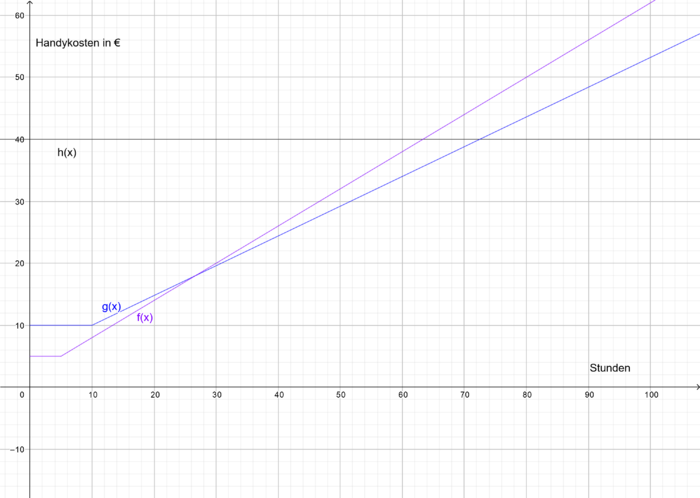
Tarif A:
Zunächst multipliziert man die 1 ct/min mit 60 min, um diesen Wert in ct/h zu haben.  min
min  ct/min
ct/min ct/h
ct/h
Nun wandelst du diesen Wert in €/h um.  ct/h
ct/h €/h. Wir kennen jetzt schon einen Teil der Funktionsgleichung.
€/h. Wir kennen jetzt schon einen Teil der Funktionsgleichung. , wobei a ein noch unbekannter Wert ist.
, wobei a ein noch unbekannter Wert ist.
Wir wissen, dass die ersten 5 Stunden frei sind,d.h hier muss nur die Grundgebühr von 5€ bezahlt werden. Der Punkt  muss also auf dem Graphen unserer Funktionsgleichung liegen. D.h. wir können diesen Punkt nun in die Funktionsgleichung von
muss also auf dem Graphen unserer Funktionsgleichung liegen. D.h. wir können diesen Punkt nun in die Funktionsgleichung von  einsetzten und nach a auflösen, um die ganze Funktionsgleichung zu erhalten.
einsetzten und nach a auflösen, um die ganze Funktionsgleichung zu erhalten.
 .
.
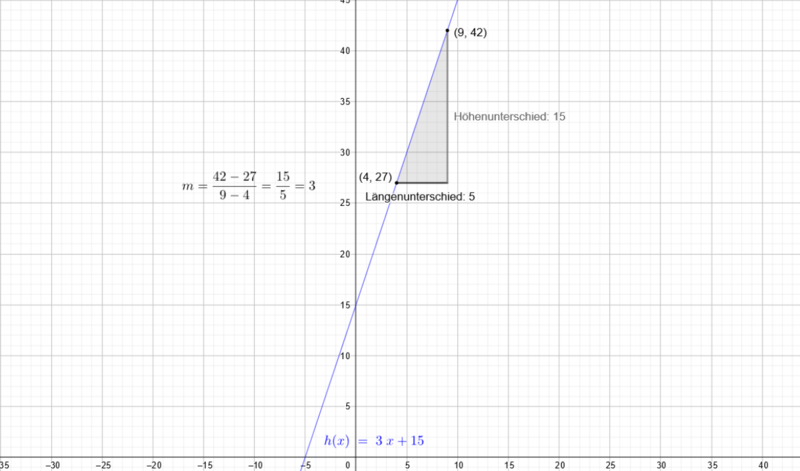
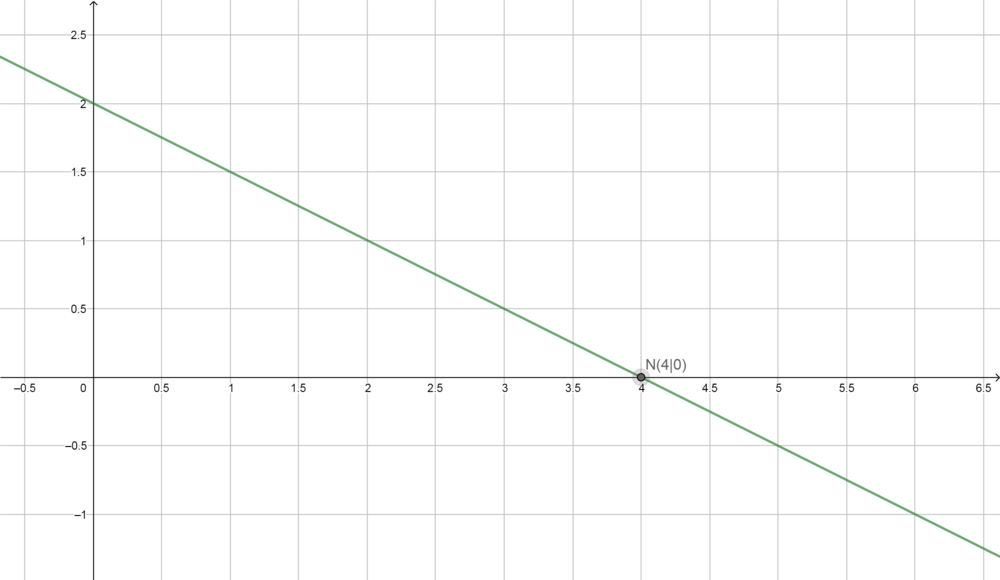
Die Funktionsgleichung für Tarif A ist also  . Beachtet jedoch, dass die Funktion bis
. Beachtet jedoch, dass die Funktion bis  konstant
konstant  ist.
ist.
Tarif B:
Zunächst multipliziert man die 0,8 ct/min mit 60 min, um diesen Wert in ct/h zu haben.  min
min  ct/min
ct/min ct/h
ct/h
Nun wandelst du diesen Wert in €/h um.  ct/h
ct/h €/h. Wir kennen jetzt schon einen Teil der Funktionsgleichung.
€/h. Wir kennen jetzt schon einen Teil der Funktionsgleichung. , wobei a ein noch unbekannter Wert ist.
, wobei a ein noch unbekannter Wert ist.
Wir wissen, dass die ersten 10 Stunden frei sind, d.h hier muss nur die Grundgebühr von 10€ bezahlt werden. Der Punkt  muss also auf dem Graphen unserer Funktionsgleichung liegen. D.h. wir können diesen Punkt nun in die Funktionsgleichung von
muss also auf dem Graphen unserer Funktionsgleichung liegen. D.h. wir können diesen Punkt nun in die Funktionsgleichung von  einsetzten und nach b auflösen, um die ganze Funktionsgleichung zu erhalten.
einsetzten und nach b auflösen, um die ganze Funktionsgleichung zu erhalten.
 .
.
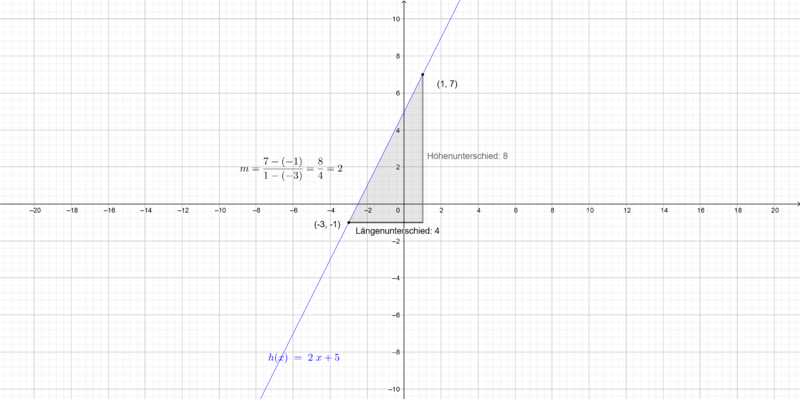
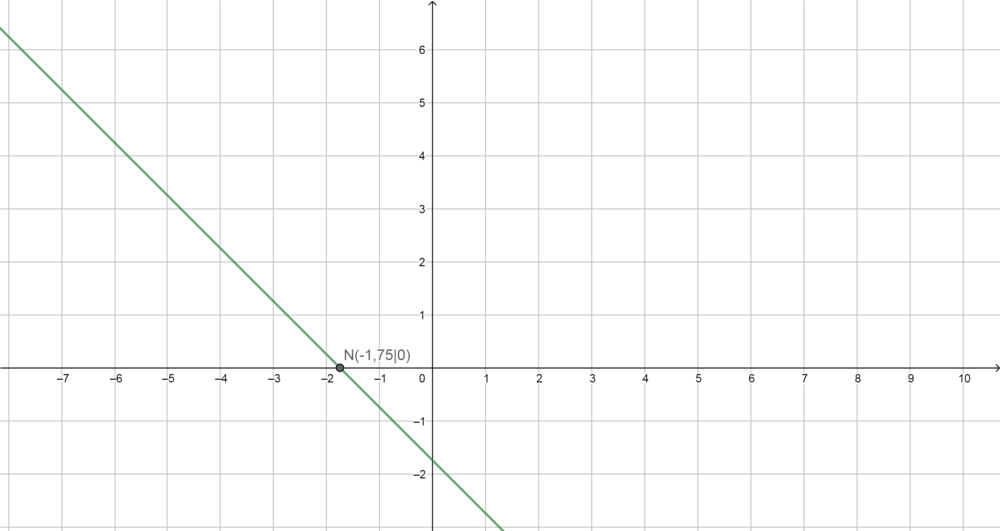
Die Funktionsgleichung für Tarif B ist also  . Beachtet jedoch, dass die Funktion bis
. Beachtet jedoch, dass die Funktion bis  konstant
konstant  ist.
ist.
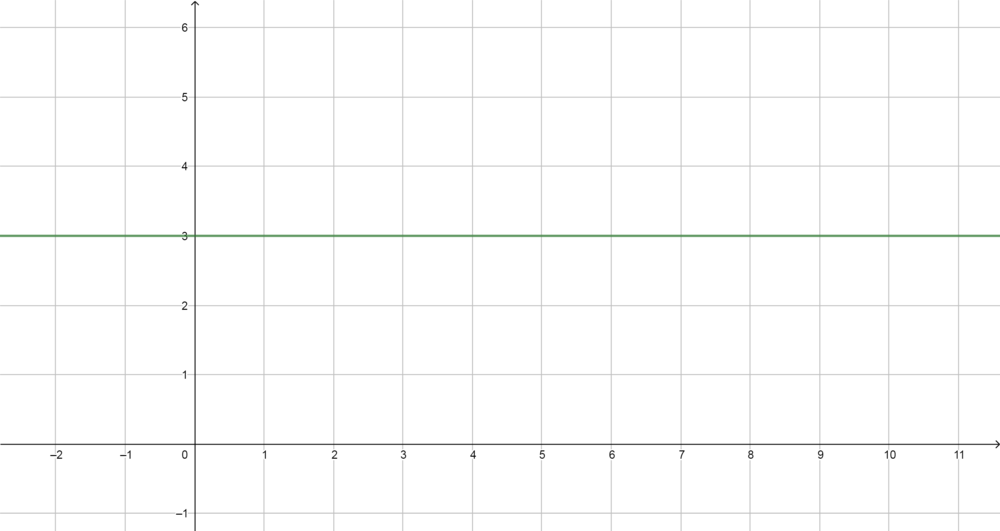
Tarif C:
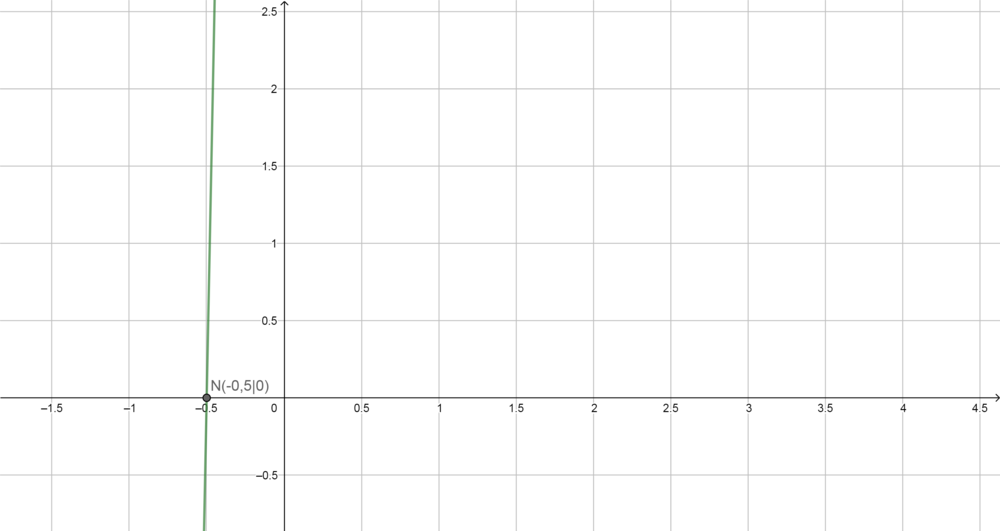
Da dies eine Flatrate ist, wird ein Wert für jeden Monat festgesetzt und dieser Wert verändert sich auch nicht wenn mehr oder weniger Stunden gesurft wird. Deshalb ist die Funktion eine Konstante.

ist die Funktionsgleichung zum Tarif C.
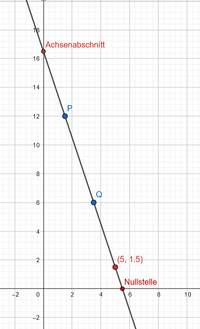
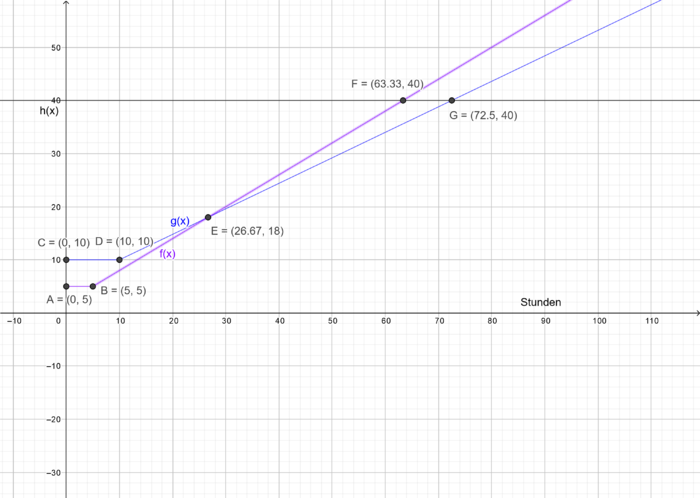
Der Schnittpunkt  sagt aus, dass der Tarif A selbst wenn man gar keine Zeit im Internet surft man dennoch
sagt aus, dass der Tarif A selbst wenn man gar keine Zeit im Internet surft man dennoch  € bezahlen muss.
€ bezahlen muss.
Der Punkt  ist uns bereits aus dem Teil a bekannt. Bis zu diesem Punkt läuft der Graph konstant, da die ersten
ist uns bereits aus dem Teil a bekannt. Bis zu diesem Punkt läuft der Graph konstant, da die ersten  Stunden frei sind, danach verläuft die Funktion linear.
Stunden frei sind, danach verläuft die Funktion linear.
Der Punkt  ist beim Tarif B der Schnittpunkt mit der
ist beim Tarif B der Schnittpunkt mit der  -Achse. Auch hier gilt also, dass selbst wenn Maria gar nicht im Internet surft sie dennoch
-Achse. Auch hier gilt also, dass selbst wenn Maria gar nicht im Internet surft sie dennoch  € bezahlen muss.
€ bezahlen muss.
Den Punkt  kennen wir schon aus dem Teil a dieser Aufgabe. Bis zu diesem Punkt läuft die Funktion des Tarifs B konstant, da die ersten
kennen wir schon aus dem Teil a dieser Aufgabe. Bis zu diesem Punkt läuft die Funktion des Tarifs B konstant, da die ersten  Stunden frei sind.
Stunden frei sind.
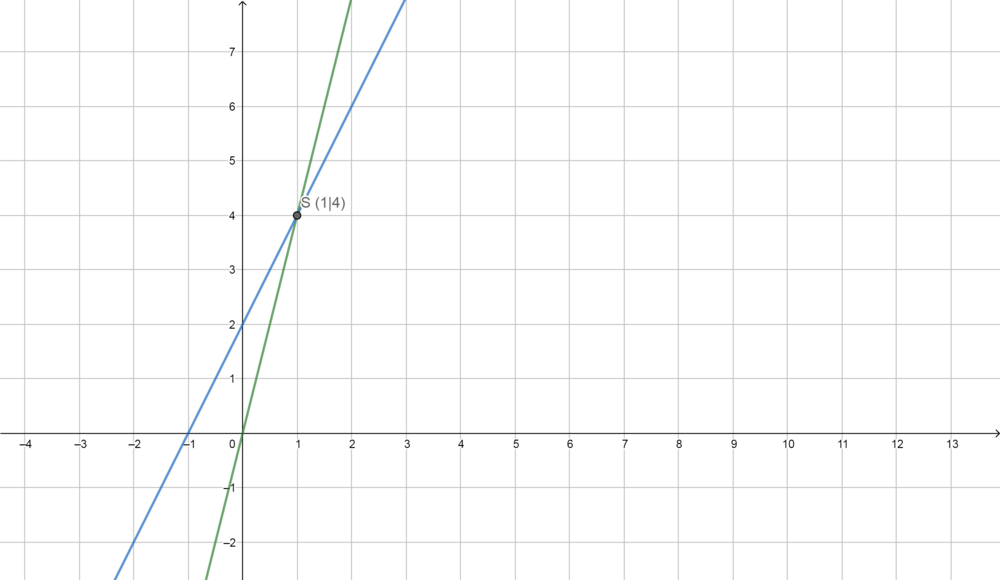
Der Punkt  ist der Schnittpunkt der beiden Funktion
ist der Schnittpunkt der beiden Funktion  und
und  . Das heißt an diesem Punkt sind die Tarife für Maria gleich teuer.
. Das heißt an diesem Punkt sind die Tarife für Maria gleich teuer.
Der Punkt ist der Schnittpunkt der Funktionen
ist der Schnittpunkt der Funktionen  und
und  . An diesem Punkt sind die beiden Tarife A und C also gleich teuer für Maria.
. An diesem Punkt sind die beiden Tarife A und C also gleich teuer für Maria.
Der Punkt  ist der Schnittpunkt der Funktionen
ist der Schnittpunkt der Funktionen  und
und  . Die beiden Tarife sind in diesem Punkt gleich teuer.
. Die beiden Tarife sind in diesem Punkt gleich teuer.
Zunächst bestimmen wir die Stundenzahl, welche Maria pro Monat fürs surfen nutzt. Maria surft  h/Tag. Da ein Monat
h/Tag. Da ein Monat  Tage hat, kann man, kann man
Tage hat, kann man, kann man  und
und  multiplizieren und erhält
multiplizieren und erhält  h/Monat.
h/Monat.
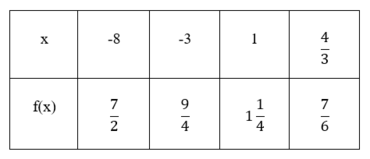
Nun setzten wir die  h als
h als  - Wert in die Funktionsgleichungen von
- Wert in die Funktionsgleichungen von  ,
,  und
und  ein und vergleichen das Ergebnis.
ein und vergleichen das Ergebnis.



Da Maria circa

h im Monat surft wäre der Tarif B mit

€ am günstigsten für sie.
Hier ist nach dem Schnittpunkt von  und
und  gefragt. Dazu setzt man die Gleichungen gleich und löst sie nach
gefragt. Dazu setzt man die Gleichungen gleich und löst sie nach  auf.
auf.

In dem Punkt

sind die Tarife A und B kostengleich.
Um dies herauszufinden brauchen wir die Schnittpunkte der Funktionsgleichungen  ,
, mit
mit  , da f und g danach größer als h sind und somit h (also der Tarif C) dann der günstigste wäre.
, da f und g danach größer als h sind und somit h (also der Tarif C) dann der günstigste wäre.


Man kann also sehen, dass der Tarif A bereits bei circa

h teurer wird als Tarif C. Der Tarif B ist bei

gleich teuer wie Tarif C. Also ab circa

h Internet Nutzung ist der Tarif C der günstigste.