Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen Teil2: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 184: | Zeile 184: | ||
|- | |- | ||
!Merksätze | !Merksätze | ||
{{Box|1=Nullstellen quadratischer Funktionen berechnen|2=Die Nullstellen sind die Schnittpunkte der Parabel mit der x-Achse, also gilt immer '''f(x) = 0'''. | |{{Box|1=Nullstellen quadratischer Funktionen berechnen|2=Die Nullstellen sind die Schnittpunkte der Parabel mit der x-Achse, also gilt immer '''f(x) = 0'''. | ||
Du erhältst also immer eine quadratische Gleichung (rein quadratisch oder gemischt quadratisch). Wie du diese löst, hast du im 1. Themenblock erarbeitet, es sind zur Wiederholung jeweils Beispiele notiert.|3=Merksatz}} | Du erhältst also immer eine quadratische Gleichung (rein quadratisch oder gemischt quadratisch). Wie du diese löst, hast du im 1. Themenblock erarbeitet, es sind zur Wiederholung jeweils Beispiele notiert.|3=Merksatz}} | ||
<u><big>1. Form: f(x) = ax² </big></u><br> | <u><big>1. Form: f(x) = ax² </big></u><br> | ||
Version vom 20. März 2025, 02:51 Uhr
Schulbuch: Schnittpunkt Mathematik 10 - Differenzierende Ausgabe, Klett-Verlag
Funktionen: Quadratische Funktionen
Einstiegstest: Quadratische Funktionen (hilfsmittelfreier Teil)
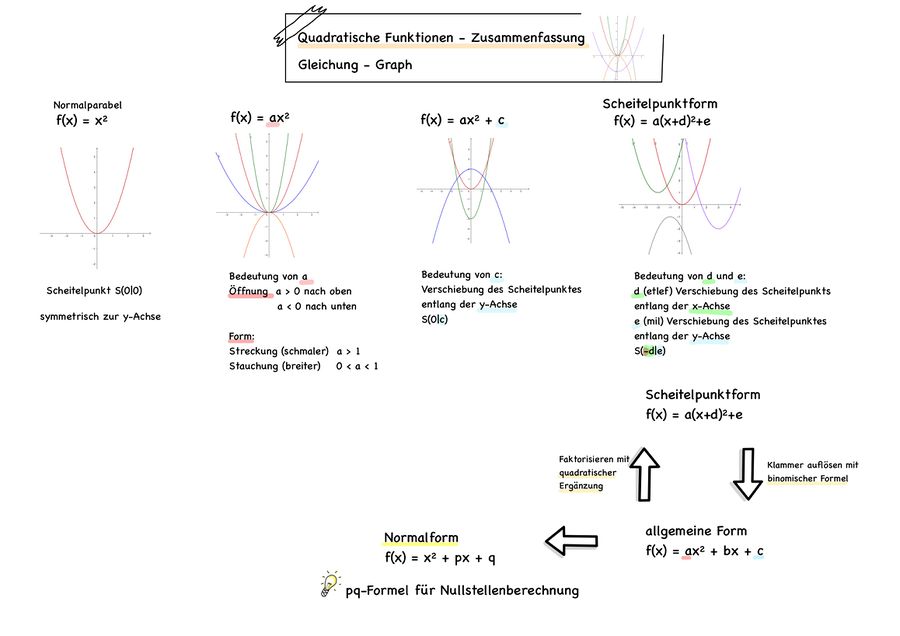
Quadratische Funktionen
Die Scheitelpunktform quadratischer Funktionen
Quadratische Funktionen: Scheitelpunktform und Normalform
| Merksätze | Du kannst die Formen der Quadratischen Funktionen umwandeln: Von der Scheitelpunktform zur Normalform |
|---|---|
| Videos | |
| Übungen |
|
Quadratische Funktionen: Nullstellen bestimmen
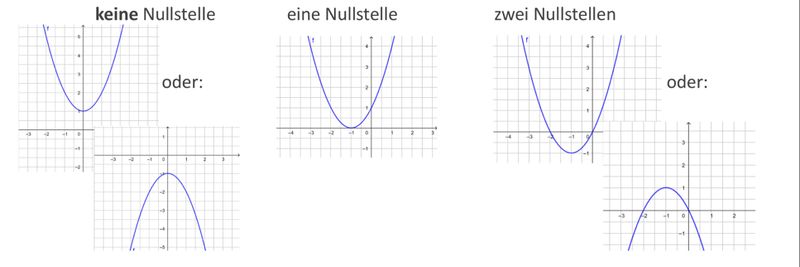
| Merksätze | Ist die Parabelgleichung in der Scheitelpunktform gegeben, kannst du die Anzahl der Nullstellen erkennen. Je nach Lage des Scheitelpunktes und der Öffnung der Parabel hat diese keine, eine oder zwei Nullstellen: | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Video | |||||||||||||
| Übung |
Tipp: Bestimme zunächst die Lage des Scheitelpunktes und die Öffnungsrichtung der Parabel. Ordne dann passend zu:
|
| Merksätze |
1. Form: f(x) = ax² Natürlich hat jede Parabel mit der Funktionsgleichung f(x) = ax² die Nullstelle N(0|0), denn ihr Scheitelpunkt liegt im Ursprung. Der Scheitelpunkt ist also die Nullstelle. 2. Form: f(x) = ax² + c Beispiel: f(x) = 0,5x² - 8 f(x) = 0 3. Form: Scheitelpunktform f(x) = a(x+d)²+e Beispiel: f(x) = 2(x + 2)² - 18
Beispiel: f(x) = x² -6x + 5 4. Form: Normalform f(x) = x² + px + q (mit quadratischer Ergänzung ) Beispiel: f(x) = x² -6x + 5 5. Form: allgemeine Form f(x) = ax² + bx + c Beispiel: f(x) = 2x² + 12x + 10 |
|---|---|
| Video | |
| Übung |
Quadratische Funktionen: Funktionsgleichung aufstellen
| Merksätze |
Beispiel: |
|---|---|
| Video | |
| Übung |
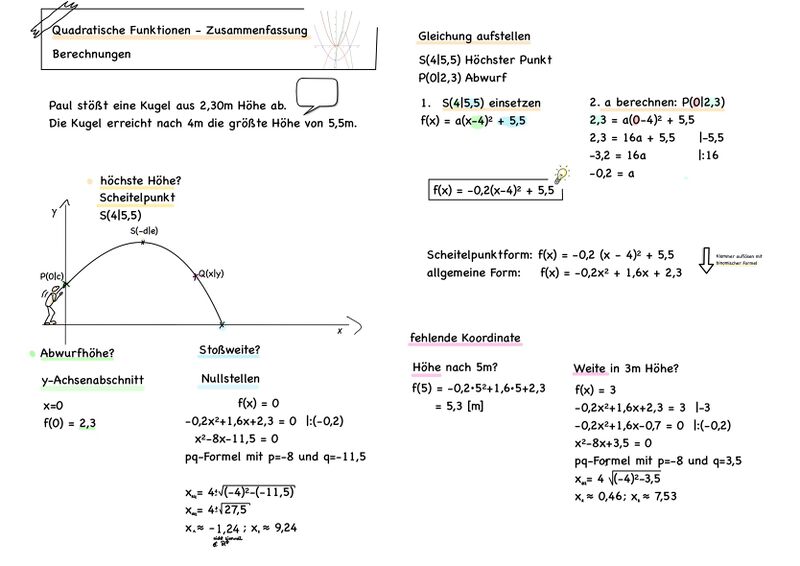
Modellieren - Anwendungsaufgaben
Es gibt besondere Punkte, die in Anwendungen immer wieder von Bedeutung sind:
- Scheitelpunkt
- Nullstellen
- Schnittpunkt mit der y-Achse
- Koordinaten eines beliebigen Punktes
Verwende zur Lösung der Aufgabe die verschiedenen Darstellungsformen und die wiederholten Methoden zur Berechnung der verschiedenen besonderen Punkte.